Laws of Motion 4 Question 10
10. A hemispherical bowl of radius $R=0.1 m$ is rotating about its own axis (which is vertical) with an angular velocity $\omega$. A particle of mass $10^{-2} kg$ on the frictionless inner surface of the bowl is also rotating with the same $\omega$. The particle is at a height $h$ from the bottom of the bowl.
$(1993,3+2 M)$
Show Answer
Answer:
Correct Answer: 10. (a) $h=R-\frac{g}{\omega^{2}}, \omega _{\min }=\sqrt{\frac{g}{R}}=9.89 rad / s$
(b) $9.8 \times 10^{-3} m / s^{2}$
Solution:
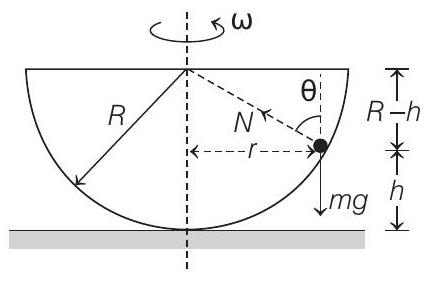
Given, $R=0.1 m, m=10^{-2} kg$
(a) FBD of particle in ground frame of reference is shown in figure. Hence,
and $\quad N \sin \theta=m r \omega^{2}$
Dividing Eq. (ii) by Eq. (i), we obtain
$$ \begin{aligned} \tan \theta & =\frac{r \omega^{2}}{g} \text { or } \frac{r}{R-h}=\frac{r \omega^{2}}{g} \\ \text { or } \quad \omega^{2} & =\frac{g}{R-h} \end{aligned} $$
This is the desired relation between $\omega$ and $h$. From Eq. (iii),
$$ h=R-\frac{g}{\omega^{2}} $$
For non-zero value of $h$,
$$ R>\frac{g}{\omega^{2}} \text { or } \omega>\sqrt{g / R} $$
Therefore, minimum value of $\omega$ should be
or
$$ \begin{aligned} \omega _{\min } & =\sqrt{\frac{g}{R}}=\sqrt{\frac{9.8}{0.1}} rad / s \\ \omega _{\min } & =9.89 rad / s \end{aligned} $$
(b) Eq. (iii) can be written as $h=R-\frac{g}{\omega^{2}}$
If $R$ and $\omega$ are known precisely, then $\Delta h=-\frac{\Delta g}{\omega^{2}}$
or $\Delta g=\omega^{2} \Delta h$ (neglecting the negative sign)
$$ (\Delta g) _{\min }=\left(\omega _{\min }\right)^{2} \Delta h,(\Delta g) _{\min }=9.8 \times 10^{-3} m / s^{2} $$
