Laws of Motion 4 Question 1
1. Two particles $A$ and $B$ are moving on two concentric circles of radii $R_{1}$ and $R_{2}$ with equal angular speed $\omega$. At $t=0$, their positions and direction of motion are shown in the figure. The relative velocity $\mathbf{v}_ {A}-\mathbf{v}_ {B}$ at $t=\frac{\pi}{2 \omega}$ is given by
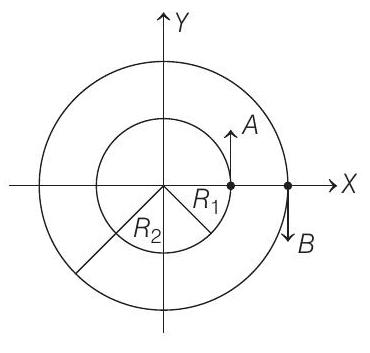
(2019 Main, 12 Jan II)
(a) $\omega\left(R_{1}+R_{2}\right) \hat{\mathbf{i}}$
(b) $-\omega\left(R_{1}+R_{2}\right) \hat{\mathbf{i}}$
(c) $\omega\left(R_{1}-R_{2}\right) \hat{\mathbf{i}}$
(d) $\omega\left(R_{2}-R_{1}\right) \hat{\mathbf{i}}$
Show Answer
Answer:
Correct Answer: 1. (d)
Solution:
- Angle covered by each particle in time duration 0 to $\frac{\pi}{2 \omega}$ is
$$ \theta=\omega \times t=\omega \times \frac{\pi}{2 \omega}=\frac{\pi}{2} \mathrm{rad} $$
So, positions of particles at $t=\frac{\pi}{2 \omega}$ is as shown below;
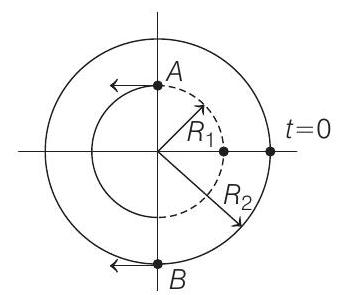
Velocities of particles at $t=\frac{\pi}{2 \omega}$ are
$$ \mathbf{v}_ {A}=-\omega R_ {1} \hat{\mathbf{i}} \quad \text { and } \quad \mathbf{v}_ {B}=-\omega R_ {2} \hat{\mathbf{i}} $$
The relative velocity of particles is
$$ \begin{aligned} \mathbf{v}_ {A}-\mathbf{v}_ {B} & =-\omega R_ {1} \hat{\mathbf{i}}-\left(-\omega R_ {2} \hat{\mathbf{i}}\right) \\ & =-\omega\left(R_ {1}-R_ {2}\right) \hat{\mathbf{i}}=\omega\left(R_{2}-R_{1}\right) \hat{\mathbf{i}} \end{aligned} $$






