Laws of Motion 4 Question 1
1. Two particles $A$ and $B$ are moving on two concentric circles of radii $R _1$ and $R _2$ with equal angular speed $\omega$. At $t=0$, their positions and direction of motion are shown in the figure. The relative velocity $\mathbf{v} _A-\mathbf{v} _B$ at $t=\frac{\pi}{2 \omega}$ is
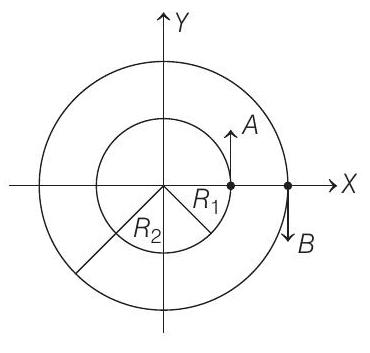given by
(2019 Main, 12 Jan II)
(a) $\omega\left(R _1+R _2\right) \hat{\mathbf{i}}$
(b) $-\omega\left(R _1+R _2\right) \hat{\mathbf{i}}$
(c) $\omega\left(R _1-R _2\right) \hat{\mathbf{i}}$
(d) $\omega\left(R _2-R _1\right) \hat{\mathbf{i}}$
Show Answer
Answer:
Correct Answer: 1. (d)
Solution:
- Angle covered by each particle in time duration 0 to $\frac{\pi}{2 \omega}$ is
$$ \theta=\omega \times t=\omega \times \frac{\pi}{2 \omega}=\frac{\pi}{2} rad $$
So, positions of particles at $t=\frac{\pi}{2 \omega}$ is as shown below;
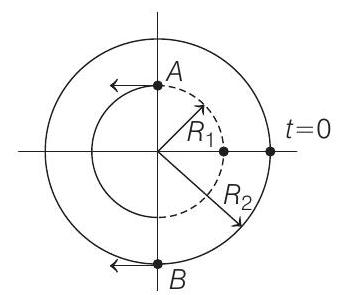
Velocities of particles at $t=\frac{\pi}{2 \omega}$ are
$$ \mathbf{v} _A=-\omega R _1 \hat{\mathbf{i}} \quad \text { and } \quad \mathbf{v} _B=-\omega R _2 \hat{\mathbf{i}} $$
The relative velocity of particles is
$$ \begin{aligned} \mathbf{v} _A-\mathbf{v} _B & =-\omega R _1 \hat{\mathbf{i}}-\left(-\omega R _2 \hat{\mathbf{i}}\right) \\ & =-\omega\left(R _1-R _2\right) \hat{\mathbf{i}}=\omega\left(R _2-R _1\right) \hat{\mathbf{i}} \end{aligned} $$
