Laws of Motion 3 Question 23
24. Two blocks connected by a massless string slides down an inclined plane having an angle of inclination of $37^{\circ}$. The masses of the two blocks are $M_{1}=4 \mathrm{~kg}$ and $M_{2}=2 \mathrm{~kg}$ respectively and the coefficients of friction of $M_{1}$ and $M_{2}$ with the inclined plane are 0.75 and 0.25 respectively. Assuming the string to be taut, find (a) the common acceleration of two masses and (b) the tension in the string. $\left(\sin 37^{\circ}=0.6, \cos 37^{\circ}=0.8\right) .\left(\right.$ Take $\left.g=9.8 \mathrm{~m} / \mathrm{s}^{2}\right)$
(1979)
Show Answer
Answer:
Correct Answer: 24. (a) $a=1.3 \mathrm{~m} / \mathrm{s}^{2}$
(b) $T=5.2 \mathrm{~N}$
Solution:
- Maximum force of friction between $M_{1}$ and inclined plane
$$ \begin{aligned} f_{1} & =\mu_{1} M_{1} g \cos \theta=(0.75)(4)(9.8)(0.8)=23.52 \mathrm{~N} \\ M_{1} g \sin \theta & =(4)(9.8)(0.6)=23.52 \mathrm{~N}=F_{1} \quad (say) \end{aligned} $$
Maximum force of friction between $M_{2}$ and inclined plane
$$ \begin{aligned} f_{2} & =\mu_{2} M_{2} g \cos \theta \\ & =(0.25)(2)(9.8)(0.8)=3.92 \mathrm{~N} \\ M_{2} g \sin \theta & =(2)(9.8)(0.6)=11.76 \mathrm{~N}=F_{2} \quad (say) \end{aligned} $$
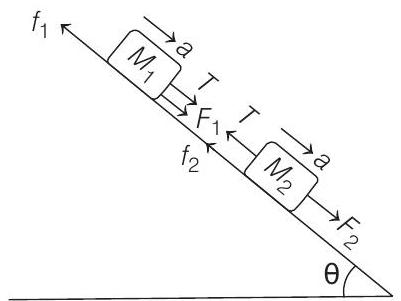
Both the blocks will be moving downwards with same acceleration $a$. Different forces acting on two blocks are as shown in above figure.
Equation of motion of $M_{1}$
$$ \text { or } \quad \begin{aligned} T+F_{1}-f_{1} & =M_{1} a \\ T & =4 a \quad \cdots(i) \end{aligned} $$
Equation of motion of $M_{2}$
$$ \begin{aligned} F_{2}-T-f_{2} & =M_{2} a \\ \text { or } \quad 7.84-T & =2 a \quad \cdots(ii) \end{aligned} $$
Solving Eqs. (i) and (ii), we get
$$ \begin{aligned} a=1.3 \mathrm{~m} / \mathrm{s}^2 \\ and && T=5.2 \mathrm{~N} \end{aligned} $$






