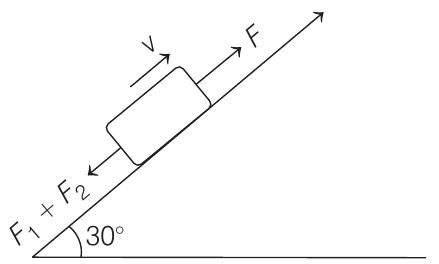
Laws of Motion 3 Question 23
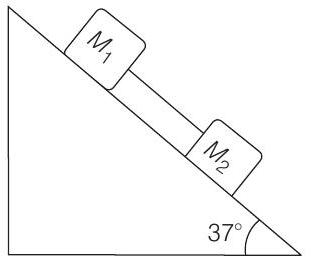
24. Two blocks connected by a massless string slides down an inclined plane having an angle of inclination of
(1979)
Show Answer
Answer:
Correct Answer: 24. (a)
(b)
Solution:
- Maximum force of friction between
Maximum force of friction between
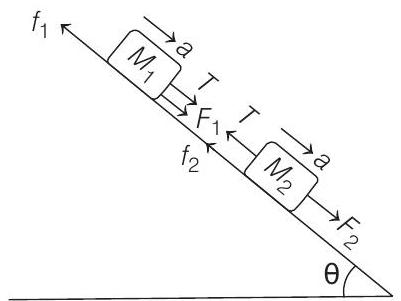
Both the blocks will be moving downwards with same acceleration
Equation of motion of
Equation of motion of
Solving Eqs. (i) and (ii), we get
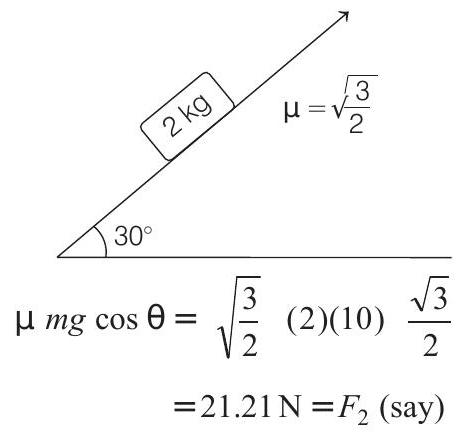
(a) Force required to move the block down the plane with constant velocity.
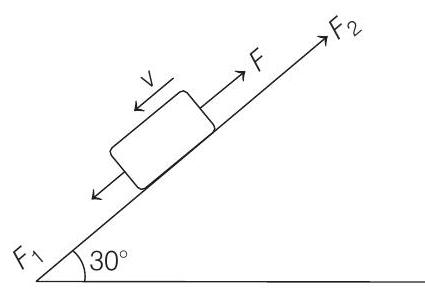
Since
(b) Force required to move the block up the plane with constant velocity.