Laws of Motion 3 Question 22
23. Masses $M_{1}, M_{2}$ and $M_{3}$ are connected by strings of negligible mass which passes over massless and frictionless pulleys $P_{1}$ and $P_{2}$ as shown in figure.
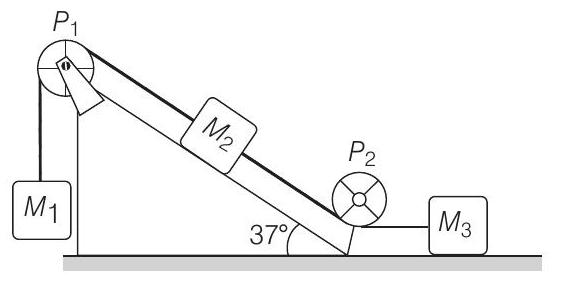
The masses move such that the portion of the string between $P_{1}$ and $P_{2}$ is parallel to the inclined plane and the portion of the string between $P_{2}$ and $M_{3}$ is horizontal. The masses $M_{2}$ and $M_{3}$ are $4.0 \mathrm{~kg}$ each and the coefficient of kinetic friction between the masses and the surfaces is 0.25 . The inclined plane makes an angle of $37^{\circ}$ with the horizontal.
If the mass $M_{1}$ moves downwards with a uniform velocity, find
(1981, 6M)
(a) the mass of $M_{1}$,
(b) the tension in the horizontal portion of the string.
(Take $g=9.8 \mathrm{~m} / \mathrm{s}^{2}, \sin 37^{\circ} \cong 3 / 5$ )
Show Answer
Answer:
Correct Answer: 23. (a) $4.2 \mathrm{~kg}$, (b) $9.8 \mathrm{~N}$
Solution:
- Constant velocity means net acceleration of the system is zero. Or net pulling force on the system is zero. While calculating the pulling force, tension forces are not taken into consideration. Therefore,
(a)
$$ \begin{aligned} M_{1} g & =M_{2} g \sin 37^{\circ}+\mu M_{2} g \cos 37^{\circ}+\mu M_{3} g \\ \text { or } \quad M_{1} & =M_{2} \sin 37^{\circ}+\mu M_{2} \cos 37^{\circ}+\mu M_{3} \end{aligned} $$
Substituting the values
$$ \begin{aligned} M_{1} & =(4) \frac{3}{5}+(0.25)(4) \frac{4}{5}+(0.25)(4) \\ & =4.2 \mathrm{~kg} \end{aligned} $$
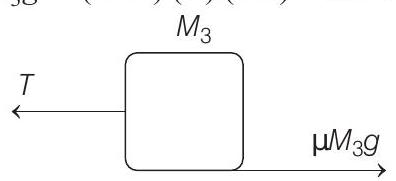
(b) Since, $M_{3}$ is moving with uniform velocity
$$ T=\mu M_{3} g=(0.25)(4)(9.8)=9.8 \mathrm{~N} $$