Laws of Motion 3 Question 1
1. Two blocks $A$ and $B$ of masses $m_{A}=1 \mathrm{~kg}$ and $m_{B}=3 \mathrm{~kg}$ are kept on the table as shown in figure. The coefficient of friction between $A$ and $B$ is 0.2 and between $B$ and the surface of the table is also 0.2 . The maximum force $F$ that can be applied on $B$ horizontally, so that the block $A$ does not slide over the block $B$ is [Take, $g=10 \mathrm{~m} / \mathrm{s}^{2}$ ]
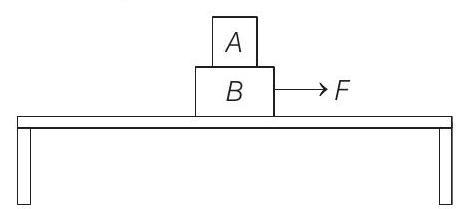
(2019 Main, 10 April II)
(a) $12 \mathrm{~N}$
(b) $16 \mathrm{~N}$
(c) $8 \mathrm{~N}$
(d) $40 \mathrm{~N}$
Show Answer
Answer:
Correct Answer: 1. (b)
Solution:
- Acceleration $a$ of system of blocks $A$ and $B$ is
$$ a=\frac{\text { Net force }}{\text { Total mass }}=\frac{F-f_{1}}{m_{A}+m_{B}} $$
where, $f_{1}=$ friction between $B$ and the surface
$$ =\mu\left(m_{A}+m_{B}\right) g $$
So,
$$ a=\frac{F-\mu\left(m_{A}+m_{B}\right) g}{\left(m_{A}+m_{B}\right)} \cdots(i) $$
Here, $\mu=0.2, m_{A}=1 \mathrm{~kg}, m_{B}=3 \mathrm{~kg}, g=10 \mathrm{~ms}^{-2}$
Substituting the above values in Eq. (i), we have
$$ \begin{aligned} & a=\frac{F-0.2(1+3) \times 10}{1+3} \\ & a=\frac{F-8}{4} \cdots(ii) \end{aligned} $$
Due to acceleration of block $B$, a pseudo force $F^{\prime}$ acts on $A$.
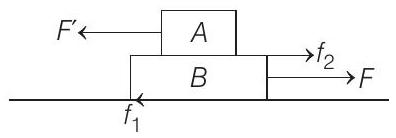
This force $F^{\prime}$ is given by $F^{\prime}=m_{A} a$
where, $a$ is acceleration of $A$ and $B$ caused by net force acting on $B$.
For $A$ to slide over $B$; pseudo force on $A$, i.e. $F^{\prime}$ must be greater than friction between $A$ and $B$.
$$ \Rightarrow \quad m_{A} a \geq f_{2} $$
We consider limiting case,
$$ \begin{aligned} & m_{A} a & =f_{2} \\ \Rightarrow \quad & m_{A} a & =\mu\left(m_{A}\right) g \\ \Rightarrow \quad & & =\mu g=0.2 \times 10=2 \mathrm{~ms}^{-2} \cdots(iii) \end{aligned} $$
Putting the value of $a$ from Eq. (iii) into Eq. (ii), we get
$$ \begin{aligned} \frac{F-8}{4} & =2 \\ \therefore \quad F & =16 \mathrm{~N} \end{aligned} $$






