Laws of Motion 3 Question 1
1. Two blocks $A$ and $B$ of masses $m _A=1 kg$ and $m _B=3 kg$ are kept on the table as shown in figure. The coefficient of friction between $A$ and $B$ is 0.2 and between $B$ and the surface of the table is also 0.2 . The maximum force $F$ that can be applied on $B$
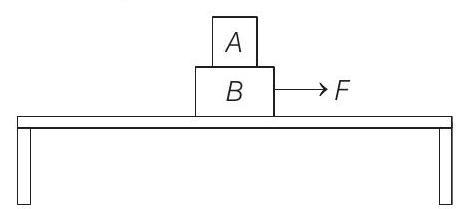horizontally, so that the block $A$ does not slide over the block $B$ is
[Take, $g=10 m / s^{2}$ ]
(2019 Main, 10 April II)
(a) $12 N$
(b) $16 N$
(c) $8 N$
(d) $40 N$
Objective Question II (One or more correct option)
Show Answer
Answer:
Correct Answer: 1. (b)
Solution:
- Acceleration $a$ of system of blocks $A$ and $B$ is
$$ a=\frac{\text { Net force }}{\text { Total mass }}=\frac{F-f _1}{m _A+m _B} $$
where, $f _1=$ friction between $B$ and the surface
$$ =\mu\left(m _A+m _B\right) g $$
So,
$$ a=\frac{F-\mu\left(m _A+m _B\right) g}{\left(m _A+m _B\right)} $$
Here, $\mu=0.2, m _A=1 kg, m _B=3 kg, g=10 ms^{-2}$
Substituting the above values in Eq. (i), we have
$$ \begin{aligned} & a=\frac{F-0.2(1+3) \times 10}{1+3} \\ & a=\frac{F-8}{4} \end{aligned} $$
Due to acceleration of block $B$, a pseudo force $F^{\prime}$ acts on $A$.
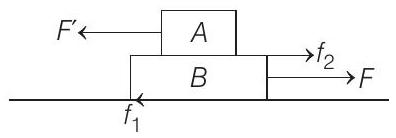
This force $F^{\prime}$ is given by $F^{\prime}=m _A a$
where, $a$ is acceleration of $A$ and $B$ caused by net force acting on $B$.
For $A$ to slide over $B$; pseudo force on $A$, i.e. $F^{\prime}$ must be greater than friction between $A$ and $B$.
$$ \Rightarrow \quad m _A a \geq f _2 $$
We consider limiting case,
$$ \begin{aligned} & m _A a & =f _2 \\ \Rightarrow \quad & m _A a & =\mu\left(m _A\right) g \\ \Rightarrow \quad & & =\mu g=0.2 \times 10=2 ms^{-2} \end{aligned} $$
Putting the value of $a$ from Eq. (iii) into Eq. (ii), we get
$$ \begin{aligned} \frac{F-8}{4} & =2 \\ \therefore \quad F & =16 N \end{aligned} $$
