Laws of Motion 2 Question 2
2. A mass of $10 \mathrm{~kg}$ is suspended vertically by a rope from the roof. When a horizontal force is applied on the mass, the rope deviated at an angle of $45^{\circ}$ at the roof point. If the suspended mass is at equilibrium, the magnitude of the force applied is (Take, $g=10 \mathrm{~ms}^{-2}$ )
(2019 Main, 9 Jan II)
(a) $70 \mathrm{~N}$
(b) $200 \mathrm{~N}$
(c) $100 \mathrm{~N}$
(d) $140 \mathrm{~N}$
Show Answer
Answer:
Correct Answer: 2. (c)
Solution:
- FBD of the given system is follow
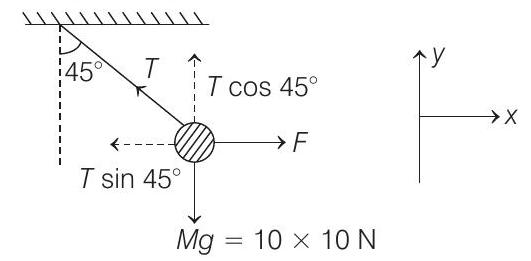
Let $T=$ tension in the rope.
For equilibrium condition of the mass,
$$ \begin{array}{lr} \Sigma F_{x}=0 & \text { (force in } x \text {-direction) } \\ \Sigma F_{y}=0 & \text { ( force in } y \text {-direction) } \end{array} $$
When $\Sigma F_{x}=0$, then
$$ \because \quad F=T \sin 45^{\circ} $$
When $\Sigma F_{y}=0$, then
$$ M g=T \cos 45^{\circ} $$
Using Eqs. (i) and (ii),
$$ \begin{aligned} & \Rightarrow \quad \frac{F}{M g}=\frac{T \sin 45^{\circ}}{T \cos 45^{\circ}} \Rightarrow \frac{F}{M g}=\frac{\frac{1}{\sqrt{2}}}{\frac{1}{\sqrt{2}}}=1 \\ & \Rightarrow \quad F=M g=10 \times 10=100 \mathrm{~N} \end{aligned} $$






