Kinematics 5 Question 16
15. A cart is moving along $x$-direction with a velocity of $4 m / s$. A person on the cart throws a stone with a velocity of $6 m / s$ relative to himself. In the frame of reference of the cart, the stone is thrown in $y-z$ plane making an angle of $30^{\circ}$ with vertical $z$-axis. At the highest point of its trajectory, the stone hits an object of equal mass hung vertically from branch of a tree by means of a string of length $L$.
A completely inelastic collision occurs, in which the stone gets embedded in the object. Determine $\left(g=9.8 m / s^{2}\right)$
(1997, 5M)
(a) the speed of the combined mass immediately after the collision with respect to an observer on the ground.
(b) the length $L$ of the string such that tension in the string becomes zero when the string becomes horizontal during the subsequent motion of the combined mass.
Show Answer
Answer:
Correct Answer: 15. (a) $2.5 m / s$
(b) $0.32 m$
Solution:
- (a) Let $\hat{\mathbf{i}}, \hat{\mathbf{j}}$ and $\hat{\mathbf{k}}$ be the unit vectors along $x, y$ and $z$-directions respectively.
$$ \begin{array}{rlrl} \text { Given, } & \mathbf{v} _{\text {cart }} & =4 \hat{\mathbf{i}} m / s \\ & \therefore \quad \mathbf{v} _{\text {stone, cart }} & =\left(6 \sin 30^{\circ}\right) \hat{\mathbf{j}}+\left(6 \cos 30^{\circ}\right) \hat{\mathbf{k}} \\ & =(3 \hat{\mathbf{j}}+3 \sqrt{3} \hat{\mathbf{k}}) m / s \\ & \therefore \quad & \mathbf{v} _{\text {stone }} & =\mathbf{v} _{\text {stone, cart }}+\mathbf{v} _{\text {cart }} \\ & & =(4 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}+3 \sqrt{3} \hat{\mathbf{k}}) m / s \end{array} $$
This is the absolute velocity of stone (with respect to ground). At highest point of its trajectory, the vertical component $(z)$ of its velocity will become zero, whereas the $x$ and $y$-components will remain unchanged. Therefore, velocity of stone at highest point will be,
$$ \mathbf{v}=(4 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}) m / s $$
or speed at highest point,
$$ v=|\mathbf{v}|=\left(\sqrt{(4)^{2}+(3)^{2}} m / s=5 m / s\right. $$
Now, applying law of conservation of linear momentum, let $v _0$ be the velocity of combined mass after collision.
$$ \begin{array}{ll} \text { Then, } & m v=(2 m) v _0 \\ \therefore & v _0=\frac{v}{2}=\frac{5}{2} m / s=2.5 m / s \end{array} $$
$\therefore$ Speed of combined mass just after collision is $2.5 m / s$.
(b) Tension in the string becomes zero at horizontal position. It implies that velocity of combined mass also becomes zero in horizontal position. Applying conservation of energy, we have
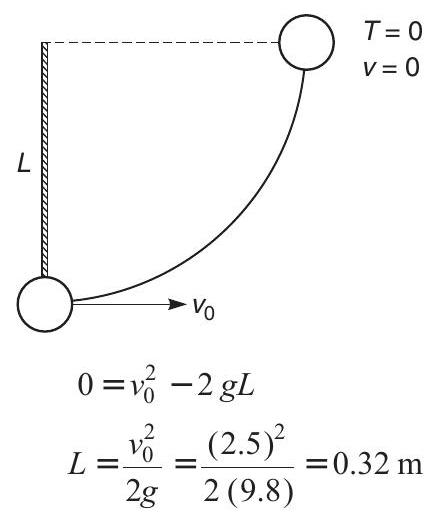
Hence, length of the string is $0.32 m$.






