Kinematics 5 Question 16
15. A cart is moving along
A completely inelastic collision occurs, in which the stone gets embedded in the object. Determine
(1997, 5M)
(a) the speed of the combined mass immediately after the collision with respect to an observer on the ground.
(b) the length
Show Answer
Answer:
Correct Answer: 15. (a)
(b)
Solution:
- (a) Let
This is the absolute velocity of stone (with respect to ground). At highest point of its trajectory, the vertical component
or speed at highest point,
Now, applying law of conservation of linear momentum, let
(b) Tension in the string becomes zero at horizontal position. It implies that velocity of combined mass also becomes zero in horizontal position. Applying conservation of energy, we have
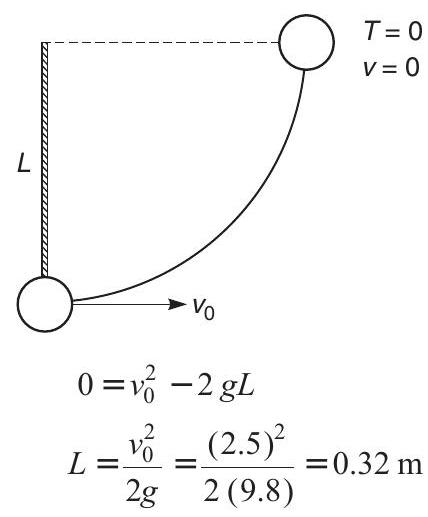
Hence, length of the string is






