Kinematics 4 Question 9
9. A particle of mass $m$ moves on the $x$-axis as follows : it starts from rest at $t=0$ from the point $x=0$ and comes to rest at $t=1$ at the point $x=1$. No other information is available about its motion at intermediate times $(0<t<1)$. If $\alpha$ denotes the instantaneous acceleration of the particle, then
(1993, 2M)
(a) $\alpha$ cannot remain positive for all $t$ in the interval $0 \leq t \leq 1$
(b) $|\alpha|$ cannot exceed 2 at any point in its path
(c) $|\alpha|$ must be $\geq 4$ at some point or points in its path
(d) $\alpha$ must change sign during the motion, but no other assertion can be made with the information given
(1984, 2M)
Show Answer
Answer:
Correct Answer: 9. (c)
Solution:
- Since, the body is at rest at $x=0$ and $x=1$. Hence, $\alpha$ cannot be positive for all time in the interval $0 \leq t \leq 1$.
Therefore, first the particle is accelerated and then retarded.
Now, total time $t=1 s$ (given)
Total displacement, $s=1 m$ (given)
$$ s=\text { Area under } v \text { - } t \text { graph } $$
$\therefore \quad$ Height or $v _{\max }=\frac{2 s}{t}=2 m / s$ is also fixed.
$$ \text { [Area or } \left.s=\frac{1}{2} \times t \times v _{\max }\right] $$
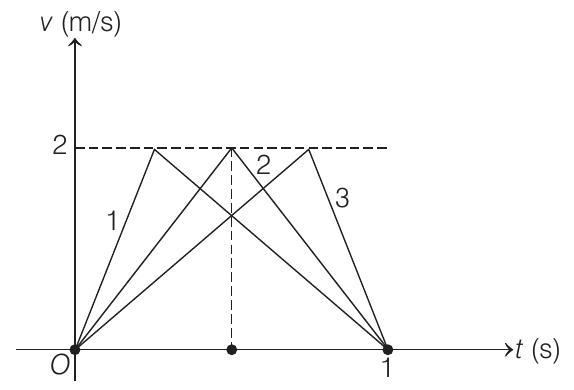
If height and base are fixed, area is also fixed .
In case $2:$ Acceleration $=$ Retardation $=4 m / s^{2}$
In case 1 : Acceleration $>4 m / s^{2}$ while
Retardation $<4 m / s^{2}$
While in case 3 : Acceleration $<4 m / s^{2}$ and
Retardation $>4 m / s^{2}$
Hence, $|\alpha| \geq 4$ at some point or points in its path.
