Kinematics 4 Question 9
9. On a frictionless horizontal surface, assumed to be the $x-y$ plane, a small trolley $A$ is moving along a straight line parallel to the $y$-axis (see figure) with a constant velocity of $(\sqrt{3}-1) m / s$. At a particular instant when the line $O A$ makes an angle of $45^{\circ}$ with the $x$-axis, a ball is thrown along the surface from the origin $O$. Its velocity makes an angle $\varphi$ with the $x$-axis and it hits the trolley.
$(2002,5$ M)
(a) The motion of the ball is observed from the frame of the trolley. Calculate the angle $\theta$ made by the velocity vector of the ball with the $x$-axis in this frame.
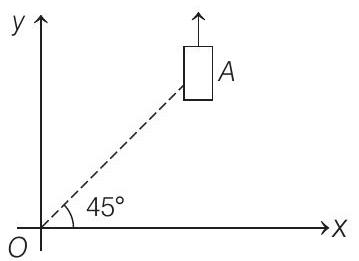
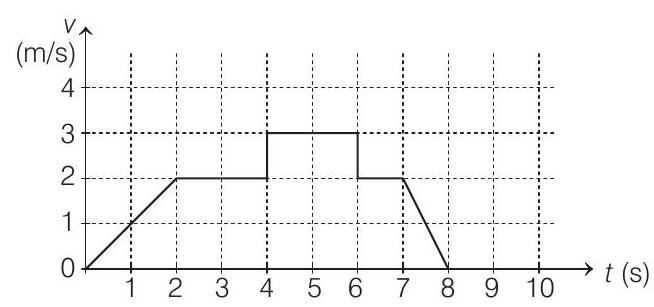
(b) Find the speed of the ball with respect to the surface, if $\varphi=4 \theta / 3$.
(a) $6 m$
(b) $3 m$
(c) $10 m$
(d) $9 m$
Show Answer
Solution:
- Since, the body is at rest at $x=0$ and $x=1$. Hence, $\alpha$ cannot be positive for all time in the interval $0 \leq t \leq 1$.
Therefore, first the particle is accelerated and then retarded.
Now, total time $t=1 s$ (given)
Total displacement, $s=1 m$ (given)
$$ s=\text { Area under } v \text { - } t \text { graph } $$
$\therefore \quad$ Height or $v _{\max }=\frac{2 s}{t}=2 m / s$ is also fixed.
$$ \text { [Area or } \left.s=\frac{1}{2} \times t \times v _{\max }\right] $$
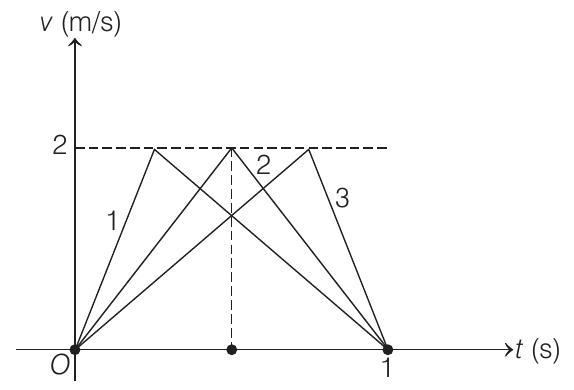
If height and base are fixed, area is also fixed .
In case $2:$ Acceleration $=$ Retardation $=4 m / s^{2}$
In case 1 : Acceleration $>4 m / s^{2}$ while
Retardation $<4 m / s^{2}$
While in case 3 : Acceleration $<4 m / s^{2}$ and
Retardation $>4 m / s^{2}$
Hence, $|\alpha| \geq 4$ at some point or points in its path.
