Kinematics 3 Question 3
3. A person standing on an open ground hears the sound of a jet aeroplane, coming from north at an angle $60^{\circ}$ with ground level. But he finds the aeroplane right vertically above his position. If $v$ is the speed of sound, then speed of the plane is
(2019 Main, 12 Jan I)
(a) $\frac{\sqrt{3}}{2} v$
(b) $v$
(c) $\frac{2 v}{\sqrt{3}}$
(d) $\frac{v}{2}$
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
- Let $P _1$ be the position of plane at $t=0$, when sound waves started towards person $A$ and $P _2$ is the position of plane observed at time instant $t$ as shown in the figure below.
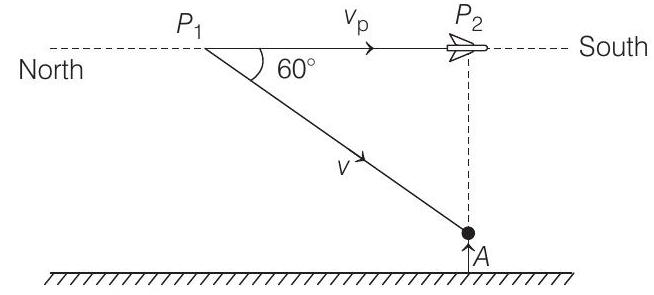
In triangle $P _1 P _2 A$,
$P _1 P _2=$ speed of plane $\times$ time $=v _P \times t$
$P _1 A=$ speed of sound $\times$ time $=v \times t$
Now, from $\Delta P _1 P _2 A$
$$ \begin{aligned} \cos \theta= & \text { base } \\ \cos 60^{\circ}=\frac{P _1 P _2}{P _1 A} & =\frac{v _P \times t}{v \times t} \\ \frac{1}{2} & =\frac{v _P}{v} \\ v _P & =\frac{v}{2} \end{aligned} $$






