Kinematics 3 Question 3
3. A person standing on an open ground hears the sound of a jet aeroplane, coming from north at an angle
(a)
(b)
(c)
(d)
figure). The length of a chamber inside the rocket is
(2014 Adv.)

Analytical & Descriptive Questions
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
- Let
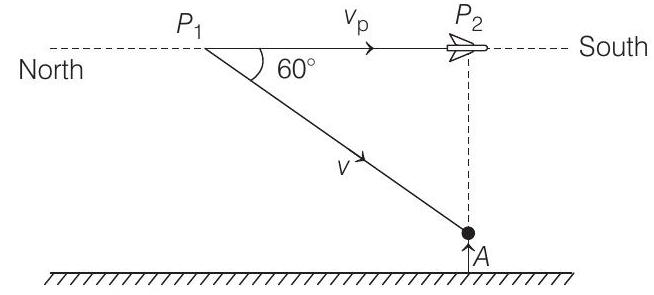
In triangle
Now, from






