Kinematics 3 Question 2
2. Ship $A$ is sailing towards north-east with velocity $\mathbf{v}=30 \hat{\mathbf{i}}+50 \hat{\mathbf{j}} km / h$, where $\hat{\mathbf{i}}$ points east and $\hat{\mathbf{j}}$ north. Ship $B$ is at a distance of $80 km$ east and $150 km$ north of Ship $A$ and is sailing towards west at $10 km / h$. $A$ will be at minimum distance from $B$ in
(2019 Main, 8 April I)
(a) $4.2 h$
(b) $2.6 h$
(c) $3.2 h$
(d) $2.2 h$
Show Answer
Answer:
Correct Answer: 2. (b)
Solution:
- Considering the initial position of ship $A$ as origin, so the velocity and position of ship will be
$$ \mathbf{v} _A=(30 \hat{\mathbf{i}}+50 \hat{\mathbf{j}}) \text { and } \mathbf{r} _A=(0 \hat{\mathbf{i}}+0 \hat{\mathbf{j}}) $$
Now, as given in the question, velocity and position of ship $B$ will be, $\mathbf{v} _B=-10 \hat{\mathbf{i}}$ and $\mathbf{r} _B=(80 \hat{\mathbf{i}}+150 \hat{\mathbf{j}})$ Hence, the given situation can be represented graphically as
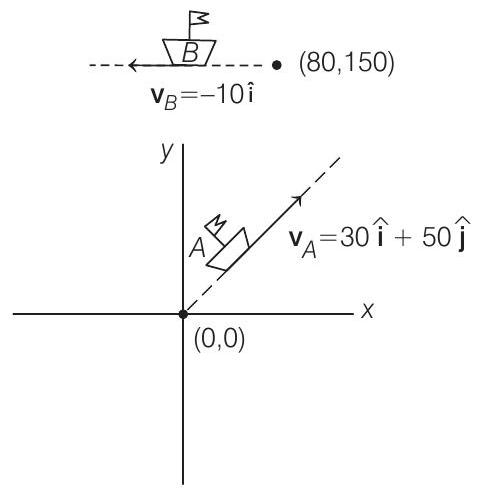
After time $t$, coordinates of ships $A$ and $B$ are
$$ (80-10 t, 150) \text { and }(30 t, 50 t) $$
So, distance between $A$ and $B$ after time $t$ is
$$ \begin{gathered} d=\sqrt{\left(x _2-x _1\right)^{2}+\left(y _2-y _1\right)^{2}} \\ d=\sqrt{(80-10 t-30 t)^{2}+(150-50 t)^{2}} \\ \Rightarrow \quad d^{2}=(80-40 t)^{2}+(150-50 t)^{2} \end{gathered} $$
Distance is minimum when $\frac{d}{d t}\left(d^{2}\right)=0$
After differentiating, we get
$$ \begin{array}{lc} \Rightarrow & \frac{d}{d t}\left[(80-40 t)^{2}+(150-50 t)^{2}\right]=0 \\ \Rightarrow & 2(80-40 t)(-40)+2(150-50 t)(-50)=0 \\ \Rightarrow & -3200+1600 t-7500+2500 t=0 \\ \Rightarrow & 4100 t=10700 \Rightarrow t=\frac{10700}{4100}=2.6 h \end{array} $$






