Kinematics 3 Question 2
2. Ship
(2019 Main, 8 April I)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 2. (b)
Solution:
- Considering the initial position of ship
Now, as given in the question, velocity and position of ship 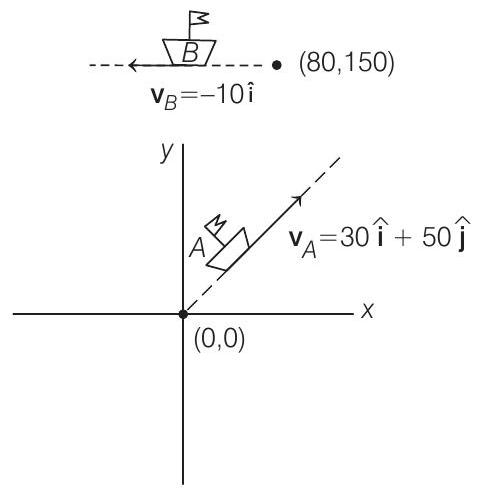
After time
So, distance between
Distance is minimum when
After differentiating, we get






