Kinematics 2 Question 7
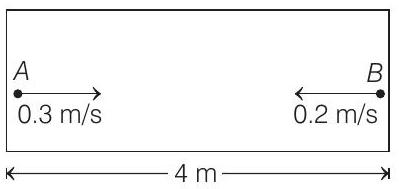
9. A rocket is moving in a gravity free space with a constant acceleration of $2 ms^{-2}$ along $+x$ direction (see figure). The length of a chamber inside the rocket is $4 \mathrm{~m}$. A ball is thrown from the left end of the chamber in $+x$ direction with a speed of $0.3 \mathrm{~ms}^{-1}$ relative to the rocket. At the same time, another ball is thrown in $-x$ direction with a speed of $0.2 \mathrm{~ms}^{-1}$ from its right end relative to the rocket. The time in seconds when the two balls hit each.
(2014 Adv.)
Show Answer
Answer:
Correct Answer: 9. $(2$ or $8)$
Solution:
Motion of ball $A$ relative to rocket.
Consider motion of two balls with respect to rocket.
Maximum distance of ball $A$ from left wall
$$ =\frac{u^{2}}{2 a}=\frac{0.3 \times 0.3}{2 \times 2}=\frac{0.09}{4} \approx 0.02 m \quad\left(\text { as } 0=u^{2}-2 a S\right) $$
So, collision of two balls will take place very near to left wall.
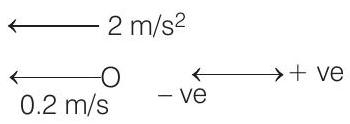
Motion of ball $B$ relative to rocket
For $B \quad S=u t+\frac{1}{2} a t^{2} \Rightarrow-4=-0.2 t-\frac{1}{2} 2 t^{2}$
Solving this equation, we get,
$$ t=1.9 s $$
$\therefore$ Nearest Integer $=2 s$
Alternate
$$ \begin{aligned} & S _1=0.2 t+\frac{1}{2} \times 2 \times t^{2} \Rightarrow S _2=0.3 t-\frac{1}{2} \times 2 \times t^{2} \\ & S _1+S _2=4 \Rightarrow 0.5 t=4 \\ \therefore \quad & t=8 s \end{aligned} $$






