Kinematics 2 Question 2
3. The bob of a simple pendulum has mass $2 \mathrm{~g}$ and a charge of $5.0 \mu \mathrm{C}$. It is at rest in a uniform horizontal electric field of intensity $2000 \mathrm{~V} / \mathrm{m}$. At equilibrium, the angle that the pendulum makes with the vertical is (take $g=10 \mathrm{~m} / \mathrm{s}^2$ )
(2019 Main, 08 April I)
(a) $\tan ^{-1}(20)$
(b) $\tan ^{-1}(0.2)$
(c) $\tan ^{-1}(5.0)$
(d) $\tan ^{-1}(0.5)$
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
- Forces on the bob are as shown
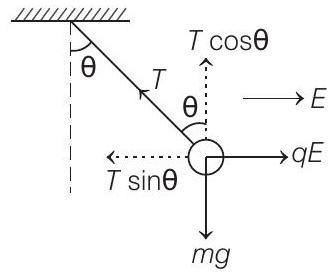
For equilibrium,
$$ \begin{aligned} T \cos \theta & =m g \cdots(i)\\ and && T \sin \theta & =q E \cdots(ii) \end{aligned} $$
$$ \tan \theta=\frac{q E}{m g} $$
Here,
$$ \begin{aligned} & q=5 \mu C=5 \times 10^{-6} C, E=2000 V / m, \\ & m=2 g=2 \times 10^{-3} kg, g=10 ms^{-2} \end{aligned} $$
$\therefore \quad \tan \theta=\frac{5 \times 10^{-6} \times 2000}{2 \times 10^{-3} \times 10}=\frac{1}{2}=0.5$
So, the angle made by the string of the pendulum with the vertical is
$$ \theta=\tan ^{-1}(0.5) $$






