Kinematics 2 Question 2
3. A particle moves in a circle of radius $R$. In half, the period of revolution its displacement is and distance covered is
(1983, 2M)
4 A particle moves from the point $(2.0 \hat{\mathbf{i}}+4.0 \hat{\mathbf{j}}) m$ at $t=0$ with an initial velocity $(5.0 \hat{\mathbf{i}}+4.0 \hat{\mathbf{j}}) ms^{-1}$. It is acted upon by a constant force which produces a constant acceleration $(4.0 \hat{\mathbf{i}}+4.0 \hat{\mathbf{j}}) ms^{-2}$. What is the distance of the particle from the origin at time $2 s$ ?
(2019 Main, 11 Jan II)
(a) $5 m$
(b) $20 \sqrt{2} m$
(c) $10 \sqrt{2} m$
(d) $15 m$
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
- Forces on the bob are as shown
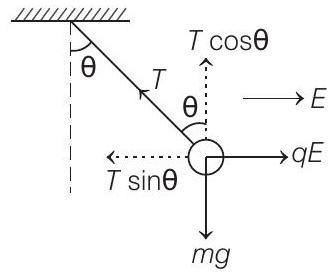
For equilibrium,
$$ \begin{aligned} T \cos \theta & =m g \\ T \sin \theta & =q E \end{aligned} $$
and
$$ \tan \theta=\frac{q E}{m g} $$
Here,
$$ \begin{aligned} & q=5 \mu C=5 \times 10^{-6} C, E=2000 V / m, \\ & m=2 g=2 \times 10^{-3} kg, g=10 ms^{-2} \end{aligned} $$
$\therefore \quad \tan \theta=\frac{5 \times 10^{-6} \times 2000}{2 \times 10^{-3} \times 10}=\frac{1}{2}=0.5$
So, the angle made by the string of the pendulum with the vertical is
$$ \theta=\tan ^{-1}(0.5) $$
