Heat and Thermodynamics 6 Question 11
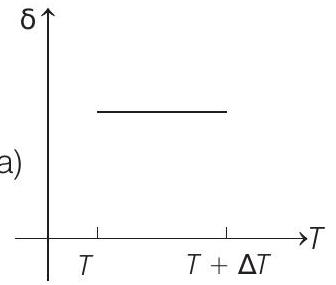
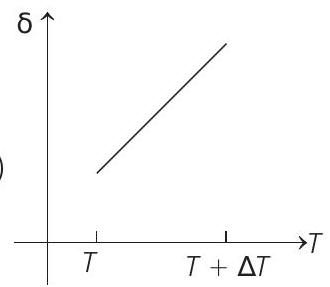
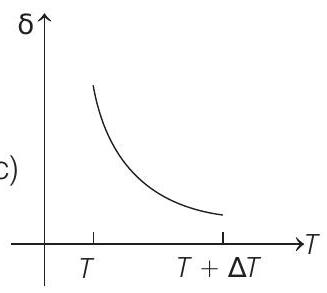
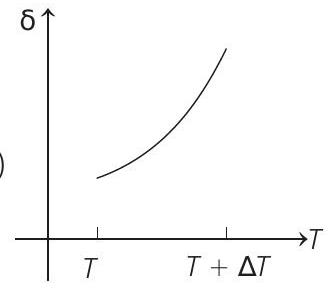
15. An ideal gas is initially at temperature $T$ and volume $V$. Its volume is increased by $\Delta V$ due to an increase in temperature $\Delta T$, pressure remaining constant. The quantity $\delta=\Delta V / V \Delta T$ varies with temperature as
(2000, 2M)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 15. (c)
Solution:
- For an ideal gas, $p V=n R T$
$$ \begin{aligned} \text { For } & p & =\text { constant } \\ & p \Delta V & =n R \Delta T \\ \therefore & \frac{\Delta V}{\Delta T} & =\frac{n R}{p}=\frac{n R}{\frac{n R T}{V}}=\frac{V}{T} \\ \therefore & \frac{\Delta V}{V \Delta T} & =\frac{1}{T} \text { or } \delta=\frac{1}{T} \end{aligned} $$
Therefore, $\delta$ is inversely proportional to temperature $T$. i.e. when $T$ increases, $\delta$ decreases and vice-versa.
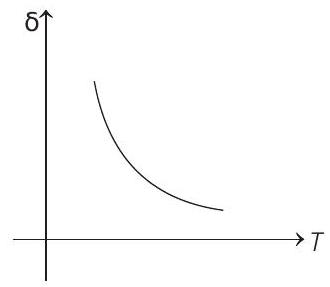
Hence, $\delta-T$ graph will be a rectangular hyperbola as shown in the above figure.






