Heat and Thermodynamics 6 Question 11
15. An ideal gas is initially at temperature $T$ and volume $V$. Its volume is increased by $\Delta V$ due to an increase in temperature $\Delta T$, pressure remaining constant. The quantity $\delta=\Delta V / V \Delta T$ varies with temperature as
(2000, 2M) (a)
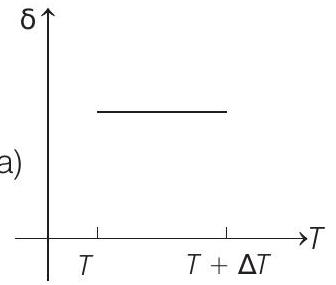
(b)
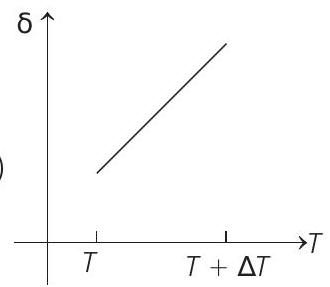
(c)
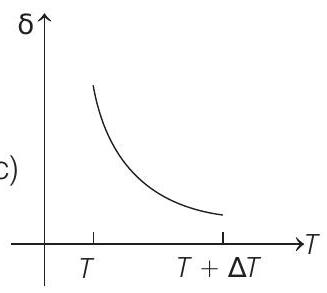
(d)
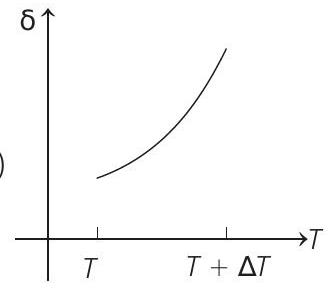
Passage Based Questions
Passage 1
In the figure a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulating material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat.
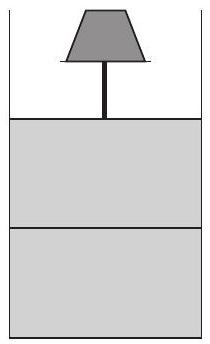
The lower compartment of the container is filled with 2 moles of an ideal monoatomic gas at $700 K$ and the upper compartment is filled with 2 moles of an ideal diatomic gas at $400 K$. The heat capacities per mole of an ideal monoatomic gas are $C _V=\frac{3}{2} R, C _p=\frac{5}{2} R$, and those for an ideal diatomic gas are $C _V=\frac{5}{2} R, C _p=\frac{7}{2} R$.
(2014 Adv.)
Show Answer
Answer:
Correct Answer: 15. Question is incomplete
Solution:
- For an ideal gas, $p V=n R T$
$$ \begin{aligned} \text { For } & p & =\text { constant } \\ & p \Delta V & =n R \Delta T \\ \therefore & \frac{\Delta V}{\Delta T} & =\frac{n R}{p}=\frac{n R}{\frac{n R T}{V}}=\frac{V}{T} \\ \therefore & \frac{\Delta V}{V \Delta T} & =\frac{1}{T} \text { or } \delta=\frac{1}{T} \end{aligned} $$
Therefore, $\delta$ is inversely proportional to temperature $T$. i.e. when $T$ increases, $\delta$ decreases and vice-versa.
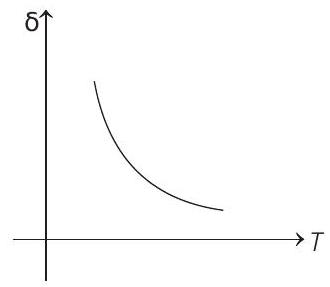
Hence, $\delta-T$ graph will be a rectangular hyperbola as shown in the above figure.






