Heat and Thermodynamics 5 Question 16
17. One mole of diatomic ideal gas undergoes a cyclic process $A B C$ as shown in figure. The process $B C$ is adiabatic. The temperatures at $A, B$ and $C$ are $400 K, 800 K$ and $600 K$, respectively. Choose the correct statement.
(2014 Main)
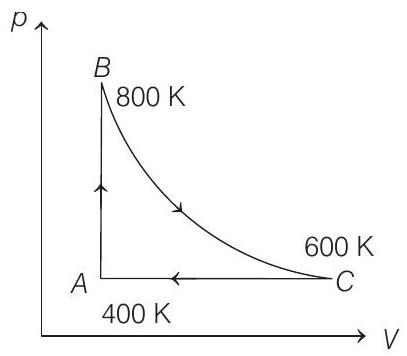
(a) The change in internal energy in whole cyclic process is $250 R$
(b) The change in internal energy in the process $C A$ is $700 R$
(c) The change in internal energy in the process $A B$ is $-350 R$
(d) The change in internal energy in the process $B C$ is $-500 R$
Show Answer
Answer:
Correct Answer: 17. (d)
Solution:
- According to first law of thermodynamics, we get
(i) Change in internal energy from $A$ to $B$ i.e. $\Delta U _{A B}$
$$ \Delta U _{A B}=n C _V\left(T _B-T _A\right)=1 \times \frac{5 R}{2}(800-400)=1000 R $$
(ii) Change in internal energy from $B$ to $C$
$$ \begin{aligned} \Delta U _{B C}=n C _V\left(T _C-T _B\right) & =1 \times \frac{5 R}{2}(600-800) \\ & =-500 R \end{aligned} $$
(iii) $\Delta U _{\text {isothermal }}=0$
(iv) Change in internal energy from $C$ to $A$ i.e. $\Delta U _{C A}$
$$ \begin{aligned} \Delta U _{C A} & =n C _V\left(T _A-T _C\right) \\ & =1 \times \frac{5 R}{2}(400-600)=-500 R \end{aligned} $$






