SATHEE: Heat and Thermodynamics 3 Question 36

Heat and Thermodynamics 3 Question 36

36. A double-pane window used for insulating a room thermally from outside consists of two glass sheets each of area $1 m^{2}$ and thickness $0.01 m$ separated by a $0.05 m$ thick stagnant air space. In the steady state, the room glass interface and the glass-outdoor interface are at constant temperatures of $27^{\circ} C$ and $0^{\circ} C$ respectively. Calculate the rate of heat flow through the window pane. Also, find the temperatures of other interfaces. Given, thermal conductivities of glass and air as 0.8 and $0.08 W m^{- 1} K^{- 1}$ respectively.

(1997C,5M)

Show Answer

Answer:

Correct Answer: 36. $41.6 W, 26.48^{\circ} C, {0.52}^{\circ} C$

Solution:

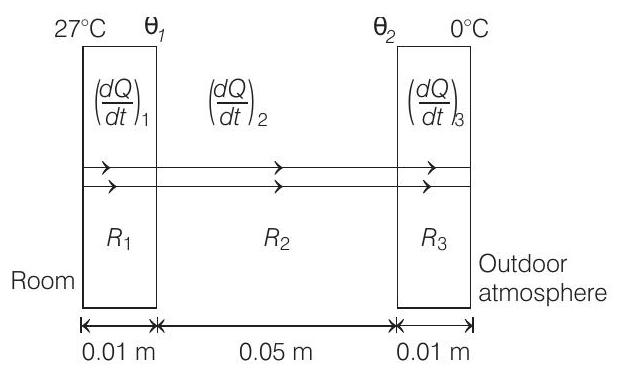
Let $θ_{1}$ and $θ_{2}$ be the temperatures of the two interfaces as shown in figure.

Thermal resistance, $R = \frac{l}{K A}$

$\begin{aligned} ∴ R_{1} = R_{3} = \frac{(0.01)}{(0.8) (1)} = 0.0125 K / W or^{\circ} C / W \\ R_{2} = \frac{(0.05)}{(0.08) (1)} = {0.625}^{\circ} C / W \end{aligned}$

Now, the rate of heat flow $(\frac{d Q}{d t})$ will be equal from all the three sections and since rate of heat flow is given by

$\frac{d Q}{d t} = \frac{Temperature difference}{Thermal resistance}$

and ${(\frac{d Q}{d t})}_{1} = {(\frac{d Q}{d t})}_{2} = {(\frac{d Q}{d t})}_{3}$

Therefore,

$\frac{27 - θ_{1}}{0.0125} = \frac{θ_{1} - θ_{2}}{0.625} = \frac{θ_{2} - 0}{0.0125}$

Solving this equation, we get

$\begin{aligned} θ_{1} & = {26.48}^{\circ} C and θ_{2} = {0.52}^{\circ} C \\ \frac{d Q}{d t} & = \frac{27 - θ_{1}}{0.0125} \Rightarrow \frac{d Q}{d t} = \frac{(27 - 26.48)}{0.0125} \\ = 41.6 W \end{aligned}$

Heat and Thermodynamics 3 Question 36

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Heat and Thermodynamics 3 Question 36

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu