Heat and Thermodynamics 3 Question 36
36. A double-pane window used for insulating a room thermally from outside consists of two glass sheets each of area $1 m^{2}$ and thickness $0.01 m$ separated by a $0.05 m$ thick stagnant air space. In the steady state, the room glass interface and the glass-outdoor interface are at constant temperatures of $27^{\circ} C$ and $0^{\circ} C$ respectively. Calculate the rate of heat flow through the window pane. Also, find the temperatures of other interfaces. Given, thermal conductivities of glass and air as 0.8 and $0.08 W m^{-1} K^{-1}$ respectively.
(1997C,5M)
Show Answer
Answer:
Correct Answer: 36. $41.6 W, 26.48{ }^{\circ} C, 0.52^{\circ} C$
Solution:
- Let $\theta _1$ and $\theta _2$ be the temperatures of the two interfaces as shown in figure.
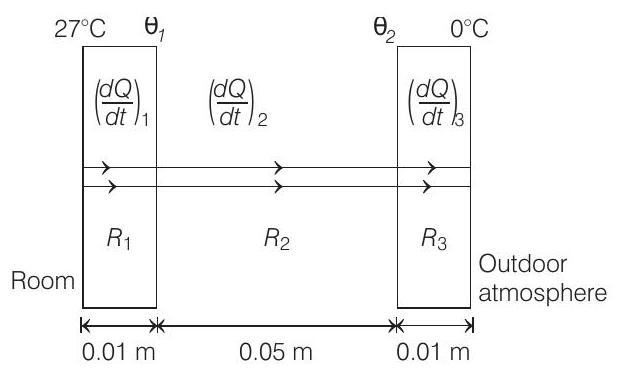
Thermal resistance, $R=\frac{l}{K A}$
$$ \begin{aligned} & \therefore \quad R _1=R _3=\frac{(0.01)}{(0.8)(1)}=0.0125 K / W \text { or }{ }^{\circ} C / W \\ & R _2=\frac{(0.05)}{(0.08)(1)}=0.625^{\circ} C / W \end{aligned} $$
Now, the rate of heat flow $\left(\frac{d Q}{d t}\right)$ will be equal from all the three sections and since rate of heat flow is given by
$$ \frac{d Q}{d t}=\frac{\text { Temperature difference }}{\text { Thermal resistance }} $$
and $\quad\left(\frac{d Q}{d t}\right) _1=\left(\frac{d Q}{d t}\right) _2=\left(\frac{d Q}{d t}\right) _3$
Therefore,
$$ \frac{27-\theta _1}{0.0125}=\frac{\theta _1-\theta _2}{0.625}=\frac{\theta _2-0}{0.0125} $$
Solving this equation, we get
$$ \begin{aligned} \theta _1 & =26.48^{\circ} C \text { and } \theta _2=0.52^{\circ} C \\ \frac{d Q}{d t} & =\frac{27-\theta _1}{0.0125} \Rightarrow \frac{d Q}{d t}=\frac{(27-26.48)}{0.0125} \\ & =41.6 W \end{aligned} $$






