Heat and Thermodynamics 2 Question 5
8. A bimetallic strip is formed out of two identical strips-one of copper and the other of brass. The coefficients of linear expansion of the two metals are $\alpha _C$ and $\alpha _B$. On heating, the temperature of the strip goes up by $\Delta T$ and the strip bends to form an arc of radius of curvature $R$. Then, $R$ is $(1999,3 M)$
(a) proportional to $\Delta T$
(b) inversely proportional to $\Delta T$
(c) proportional to $\left|\alpha _B-\alpha _C\right|$
(d) inversely proportional to $\left|\alpha _B-\alpha _C\right|$
Show Answer
Answer:
Correct Answer: 8. (b,d)
Solution:
- Let $l _0$ be the initial length of each strip before heating. Length after heating will be
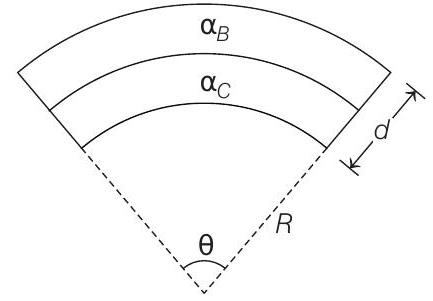
$$ \begin{aligned} & l _B=l _0\left(1+\alpha _B \Delta T\right)=(R+d) \theta \\ & l _C=l _0\left(1+\alpha _C \Delta T\right)=R \theta \end{aligned} $$
[From binomial expansion]
$$ \therefore \quad R=\frac{d}{\left(\alpha _B-\alpha _C\right) \Delta T} \quad \text { or } \quad R \propto \frac{1}{\Delta T} \propto \frac{1}{\left|\alpha _B-\alpha _C\right|} $$






