Gravitation 5 Question 3
3. Two stars of masses $3 \times 10^{31} kg$ each and at distance $2 \times 10^{11}$ $m$ rotate in a plane about their common centre of mass $O$. A meteorite passes through $O$ moving perpendicular to the star’s rotation plane. In order to escape from the gravitational field of this double star, the minimum speed that meteorite should have at $O$ is (Take, gravitational constant, $G=6.67 \times 10^{-11} N-m^{2} kg^{-2}$ ) (Main 2019, 10 Jan II)
(a) $2.8 \times 10^{5} m / s$
(b) $3.8 \times 10^{4} m / s$
(c) $2.4 \times 10^{4} m / s$
(d) $1.4 \times 10^{5} m / s$
Show Answer
Answer:
Correct Answer: 3. (a)
Solution:
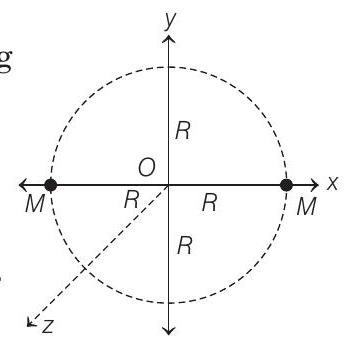
- Let us assume that stars are moving in $x y$-plane with origin as their centre of mass as shown in the figure below
According to question, mass of each star, $M=3 \times 10^{31} kg$ and diameter of circle,
$$ \begin{aligned} 2 R & =2 \times 10^{11} m \\ \Rightarrow \quad R & =10^{11} m \end{aligned} $$
Potential energy of meteorite at $O$, origin $\hat{\mathbf{j}}$ is, $\quad U _{\text {total }}=-\frac{2 G M m}{r}$
If $v$ is the velocity of meteorite at $O$ then Kinetic energy $K$ of the meteorite is
$$ K=\frac{1}{2} m v^{2} $$
To escape from this dual star system, total mechanical energy of the meteorite at infinite distance from stars must be at least zero. By conservation of energy, we have
$$ \begin{gathered} \frac{1}{2} m v^{2}-\frac{2 G M m}{R}=0 \\ \Rightarrow v^{2}=\frac{4 G M}{R}=\frac{4 \times 6.67 \times 10^{-11} \times 3 \times 10^{31}}{10^{11}} \\ \Rightarrow v=2.8 \times 10^{5} m / s \end{gathered} $$






