Gravitation 5 Question 3
3. Two stars of masses
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 3. (a)
Solution:
- Let us assume that stars are moving in
According to question, mass of each star,
Potential energy of meteorite at
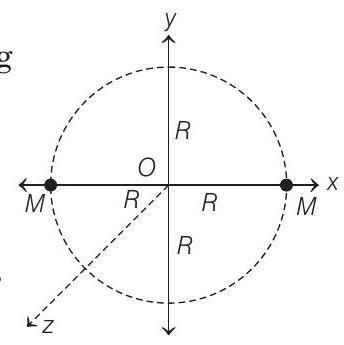
If
To escape from this dual star system, total mechanical energy of the meteorite at infinite distance from stars must be at least zero. By conservation of energy, we have






