Gravitation 2 Question 9
12. The masses and radii of the Earth and the Moon are $M_{1}, R_{1}$ and $M_{2}, R_{2}$ respectively. Their centres are a distance $d$ apart. The minimum speed with which a particle of mass $m$ should be projected from a point midway between the two centres so as to escape to infinity is
(1988, 2M)
Show Answer
Answer:
Correct Answer: 12. $v=2 \sqrt{\frac{G\left(M_{1}+M_{2}\right)}{d}}$
Solution:
- Total mechanical energy of mass $m$ at a point midway between two centres is
$$ E=-\frac{G M_{1} m}{d / 2}-\frac{G M_{2} m}{d / 2}=-\frac{2 G m}{d}\left(M_{1}+M_{2}\right) $$
Binding energy $=\frac{2 G m}{d}\left(M_{1}+M_{2}\right)$
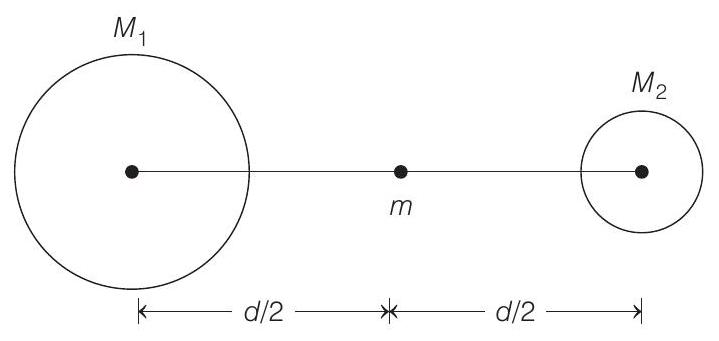
Kinetic energy required to escape the mass to infinity is,
$$ \begin{aligned} \frac{1}{2} m v_{e}^{2} & =\frac{2 G m}{d}\left(M_{1}+M_{2}\right) \\ \therefore \quad v_{e} & =2 \sqrt{\frac{G\left(M_{1}+M_{2}\right)}{d}} \end{aligned} $$






