SATHEE: Electrostatics 7 Question 23

Electrostatics 7 Question 23

25. Four point charges, each of $+ q$ , are rigidly fixed at the four corners of a square planar soap film of side $a$ . The surface tension of the soap film is $γ$ . The system of charges and planar film are in equilibrium, and $a = k {\frac{q^{2}}{Y}}^{1 / N}$ , where $k$ is a constant. Then $N$ is

(2011)

Show Answer

Answer:

Correct Answer: 25. 3

Solution:

$F_{1} =$ Net electrostatic force on any one charge due to rest of three charges

$= \frac{1}{4 π ε_{0}} \frac{q^{2}}{a^{2}} \sqrt{2} + \frac{1}{2}$

$F_{2} =$ Surface tension force $= γ a$

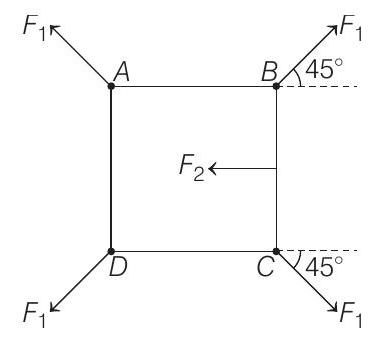
If we see the equilibrium of line $B C$ , then

$\begin{matrix} 2 F_{1} \cos 45^{\circ} = F_{2} \\ or \sqrt{2} F_{1} = F_{2} \\ or \frac{1}{4 π ε_{0}} \frac{q^{2}}{a^{2}} 2 + \frac{1}{\sqrt{2}} = γ a \\ ∴ a^{3} = \frac{1}{4 π ε_{0}} 2 + \frac{1}{\sqrt{2}} \frac{q^{2}}{Y} \\ or a = \frac{1}{4 π ε_{0}} 2 + \frac{1}{\sqrt{2}} \frac{q^{2}}{Y} = k \frac{q^{2}}{Y} \end{matrix}$

where, $k = \frac{1}{4 π ε_{0}} 2 + \frac{1}{\sqrt{2}}$

Therefore, $N = 3$

Answer is 3 .

Electrostatics 7 Question 23

Answer:

Solution:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Electrostatics 7 Question 23

25. Four point charges, each of +q, are rigidly fixed at the four corners of a square planar soap film of side a. The surface tension of the soap film is γ. The system of charges and planar film are in equilibrium, and a=kq2Y1/N, where k is a constant. Then N is

Answer:

Solution:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu