Electrostatics 7 Question 22
24. A positively charged thin metal ring of radius $R$ is fixed in the $x-y$ plane with its centre at the origin $O$. A negatively charged particle $P$ is released from rest at the point $\left(0,0, z_{0}\right)$ where $z_{0}>0$. Then the motion of $P$ is
(a) periodic for all values of $z_{0}$ satisfying $0<z_{0}<\infty$
(b) simple harmonic for all values of $z_{0}$ satisfying $0<z_{0} \leq R$
(c) approximately simple harmonic provided $z_{0}«R$
(d) such that $P$ crosses $O$ and continues to move along the negative $z$-axis towards $z=-\infty$
Show Answer
Answer:
Correct Answer: 24. (a,c)
Solution:
- Let $Q$ be the charge on the ring, the negative charge $-q$ is released from point $P\left(0,0, z_{0}\right)$. The electric field at $P$ due to the charged ring will be along positive $z$-axis and its magnitude will be
$$ E=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q z_{0}}{\left(R^{2}+z_{0}^{2}\right)^{3 / 2}} $$
$E=0$ at centre of the ring because $z_{0}=0$
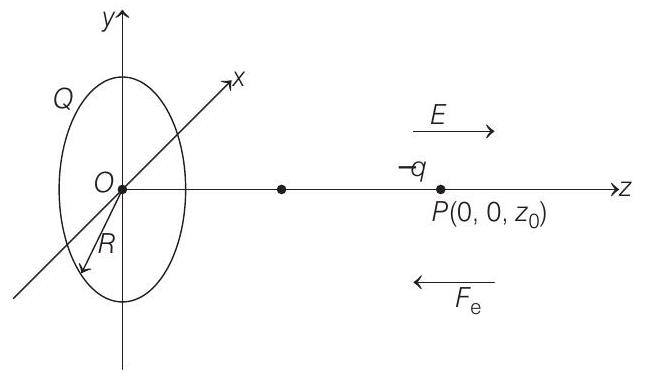
Force on charge at $P$ will be towards centre as shown, and its magnitude is
$$ F_{e}=q E=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q q}{\left(R^{2}+z_{0}^{2}\right)^{3 / 2}} \cdot z_{0} $$
Similarly, when it crosses the origin, the force is again towards centre $O$.
Thus, the motion of the particle is periodic for all values of $z_{0}$ lying between 0 and $\infty$.
Secondly, if $z_{0}«R,\left(R^{2}+z_{0}^{2}\right)^{3 / 2} \approx R^{3}$
$$ \left.F_{e} \approx \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q q}{R^{3}} \cdot z_{0} \quad \text { [From Eq. (i) }\right] $$
i.e. the restoring force $F_{e} \propto-z_{0}$. Hence, the motion of the particle will be simple harmonic. (Here negative sign implies that the force is towards its mean position.)
