Electrostatics 7 Question 2
2. An electric dipole is formed by two equal and opposite charges $q$ with separation $d$. The charges have same mass $m$. It is kept in a uniform electric field $E$. If it is slightly rotated from its equilibrium orientation, then its angular frequency $\omega$ is
(a) $\sqrt{\frac{2 q E}{m d}}$
(b) $2 \sqrt{\frac{q E}{m d}}$
(c) $\sqrt{\frac{q E}{m d}}$
(d) $\sqrt{\frac{q E}{2 m d}}$
Show Answer
Answer:
Correct Answer: 2. (a)
Solution:
- Key Idea When an electric dipole is placed in an electric field $E$ at some angle $\theta$, then two forces equal in magnitude but opposite in direction acts on the tve and $\rightarrow$ ve charges, respectively. These forces forms a couple which exert a torque, which is given as
$$ \tau=p \times E $$
where, $p$ is dipole moment.
Torque on the dipole is given as
$$ \tau=I \alpha=-p E \sin \theta $$
where, $I$ is the moment of inertia and $\alpha$ is angular acceleration.
For small angles, $\sin \theta \approx \theta$
$$ \therefore \quad \alpha=-\frac{p E}{I} \theta $$
Moment of inertia of the given system is
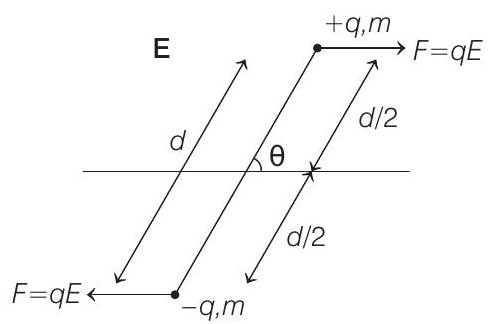
$$ I=m \frac{d}{2}^{2}+m \frac{d}{2}^{2}=\frac{2 m d^{2}}{4}=\frac{m d^{2}}{2} $$
Substituting the value of $I$ in Eq. (i), we get
$$ \Rightarrow \quad \alpha=-\frac{2 p E}{m d^{2}} \cdot \theta $$
The above equation is similar to the equation for a system executing angular SHM.
Comparing Eq. (ii), with the general equation of angular SHM, i.e.
$$ \alpha=-\omega^{2} \theta $$
where, $\omega$ is the angular frequency,
we get
$$ \begin{aligned} & \omega^{2} & =\frac{2 p E}{m d^{2}} \quad \text { or } \omega=\sqrt{\frac{2 p E}{m d^{2}}} \\ \text { As, } & p & =q d \\ \therefore & \omega & =\sqrt{\frac{2 q d E}{m d^{2}}}=\sqrt{\frac{2 q E}{m d}} \end{aligned} $$






