Electrostatics 7 Question 2
2. An electric dipole is formed by two equal and opposite charges
(a)
(b)
(c)
(d)
Show Answer
Solution:
- Key Idea When an electric dipole is placed in an electric field
where,
Torque on the dipole is given as
where,
For small angles,
Moment of inertia of the given system is
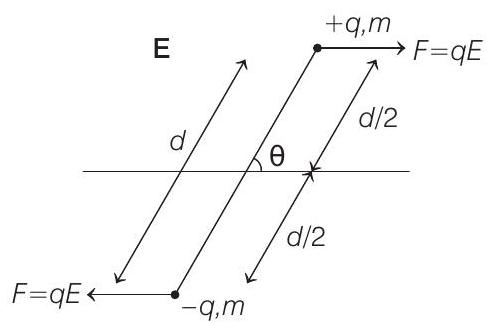
Substituting the value of
The above equation is similar to the equation for a system executing angular SHM.
Comparing Eq. (ii), with the general equation of angular SHM, i.e.
where,
we get






