Electrostatics 6 Question 13
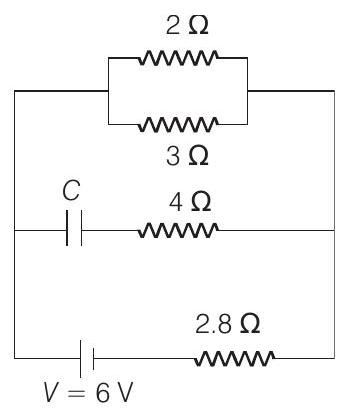
13. Calculate the steady state current in the $2 \Omega$ resistor shown in the circuit (see figure). The internal resistance of the battery is negligible and the capacitance of the condenser $C$ is $0.2 \mu \mathrm{F}$.
$(1982,5 \mathrm{M})$
Show Answer
Answer:
Correct Answer: 13. 0.9 A
Solution:
- In steady state situation no current will flow through the capacitor. $2 \Omega$ and $3 \Omega$ are in parallel.
Therefore, their combined resistance will be
$$ R=\frac{2 \times 3}{2+3}=1.2 \Omega $$
Net current through the battery
$$ i=\frac{6}{1.2+2.8}=1.5 \mathrm{~A} $$
This current will distribute in inverse ratio of their resistances in $2 \Omega$ and $3 \Omega$.
$$ \begin{array}{rlrl} \therefore & & \frac{i_{2}}{i_{3}} & =\frac{3}{2} \\ \text { or } & i_{2} & =\frac{3}{3+2} \quad(1.5)=0.9 \mathrm{~A} \end{array} $$






