Electrostatics 5 Question 7
8. Voltage rating of a parallel plate capacitor is $500 \mathrm{~V}$. Its dielectric can withstand a maximum electric field of $10^{6} \mathrm{~V} / \mathrm{m}$. The plate area is $10^{-4} \mathrm{~m}^{2}$. What is the dielectric constant, if the capacitance is $15 \mathrm{pF}$ ?
(Take, $\varepsilon_{0}=8.86 \times 10^{-12} \mathrm{C}^{2} / \mathrm{N}-\mathrm{m}^{2}$ )
(Main 2019, 8 April I)
(a) 3.8
(b) 8.5
(c) 4.5
(d) 6.2
Show Answer
Answer:
Correct Answer: 8. (b)
Solution:
- As we know, capacitance of a capacitor filled with dielectric medium,
$ C=\frac{\varepsilon_{0} K A}{d} $
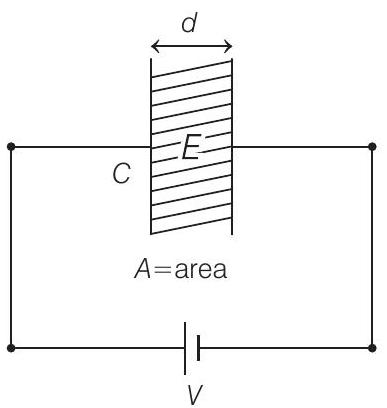
and potential difference between plates is
$ E=\frac{V}{d} \Rightarrow d=\frac{V}{E} $
So, by combining both Eqs. (i) and (ii), we get
$ K=\frac{C V}{\varepsilon_{0} A E} $
Given, $C=15 \mathrm{pF}=15 \times 10^{-12} \mathrm{~F}$,
$ V=500 \mathrm{~V}, E=10^{6} \mathrm{Vm}^{-1}, $
$ A=10^{-4} \mathrm{~m}^{2} $
and $\quad \varepsilon_{0}=8.85 \times 10^{-12} \mathrm{C}^{2} \mathrm{~N}^{-1} \mathrm{~m}^{-2}$
Substituting the values in Eq. (iii), we get
$ \begin{aligned} K & =\frac{15 \times 10^{-12} \times 500}{8.85 \times 10^{-12} \times 10^{-4} \times 10^{6}} \\ & =8.47 \approx 8.5 \end{aligned} $
