Electrostatics 5 Question 49
51. Two parallel plate capacitors $A$ and $B$ have the same separation $d=8.85 \times 10^{-4} \mathrm{~m}$ between the plates. The plate areas of $A$ and $B$ are $0.04 \mathrm{~m}^{2}$ and $0.02 \mathrm{~m}^{2}$ respectively. A slab of dielectric constant (relative permittivity) $K=9$ has dimensions such that it can exactly fill the space between the plates of capacitor $B$.
(1993, 7M)
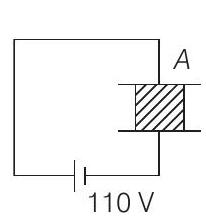
(i)
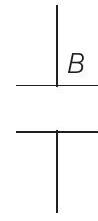
(ii)
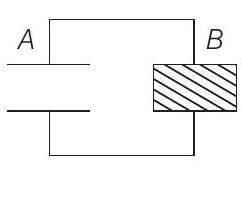
(iii)
(a) The dielectric slab is placed inside $A$ as shown in figure (i) $A$ is then charged to a potential difference of $110 \mathrm{~V}$. Calculate the capacitance of $A$ and the energy stored in it.
(b) The battery is disconnected and then the dielectric slab is removed from $A$. Find the work done by the external agency in removing the slab from $A$.
(c) The same dielectric slab is now placed inside $B$, filling it completely. The two capacitors $A$ and $B$ are then connected as shown in figure (iii). Calculate the energy stored in the system.
Show Answer
Answer:
Correct Answer: 51. (a) $C_A=2 \times 10^{-9} \mathrm{~F}, U_A=1.21 \times 10^{-5} \mathrm{~J}$
(b) $W=4.84 \times 10^{-5} \mathrm{~J}$
(c) $U=1.1 \times 10^{-5} \mathrm{~J}$
Solution:
- (a) Capacitor $A$ is a combination of two capacitors $C_{K}$ and $C_{O}$ in parallel. Hence,
$$ C_{A}=C_{K}+C_{O}=\frac{K \varepsilon_{0} A}{d}+\frac{\varepsilon_{0} A}{d}=(K+1) \frac{\varepsilon_{0} A}{d} $$
Here, $A=0.02 \mathrm{~m}^{2}$. Substituting the values, we have
$$ \begin{aligned} & C_{A}=(9+1) \frac{8.85 \times 10^{-12}(0.02)}{\left(8.85 \times 10^{-4}\right)} \\ & C_{A}=2.0 \times 10^{-9} \mathrm{~F} \end{aligned} $$
Energy stored in capacitor $A$, when connected with a $110 \mathrm{~V}$ battery is
$$ \begin{aligned} & U_{A}=\frac{1}{2} C_{A} V^{2}=\frac{1}{2}\left(2 \times 10^{-9}\right)(110)^{2} \\ & U_{A}=1.21 \times 10^{-5} \mathrm{~J} \end{aligned} $$
(b) Charge stored in the capacitor
$$ q_{A}=C_{A} V=\left(2.0 \times 10^{-9}\right)(110) \Rightarrow q_{A}=2.2 \times 10^{-7} \mathrm{C} $$
Now, this charge remains constant even after battery is disconnected. But when the slab is removed, capacitance of $A$ will get reduced. Let it be $C_{A}^{\prime}$
$$ \begin{aligned} C_{A}^{\prime}=\frac{\varepsilon_{0}(2 A)}{d} & =\frac{\left(8.85 \times 10^{-12}\right)(0.04)}{8.85 \times 10^{-4}} \\ C_{A}^{\prime} & =0.4 \times 10^{-9} \mathrm{~F} \end{aligned} $$
Energy stored in this case would be
$$ \begin{aligned} U_{A}^{\prime} & =\frac{1}{2} \frac{\left(q_{A}\right)^{2}}{C_{A}^{\prime}}=\frac{1}{2} \frac{\left(2.2 \times 10^{-7}\right)^{2}}{\left(0.4 \times 10^{-9}\right)} \\ U_{A}^{\prime} & =6.05 \times 10^{-5} \mathrm{~J}>U_{A} \end{aligned} $$
Therefore, work done to remove the slab would be
$$ \begin{array}{rlrl} & W=U_{A}^{\prime} \quad-U_{A}=(6.05-1.21) \times 10^{-5} \mathrm{~J} \\ \text { or } & W & =4.84 \times 10^{-5} \mathrm{~J} \end{array} $$
(c) Capacity of $B$ when filled with dielectric is
$$ \begin{aligned} & C_{B}=\frac{K \varepsilon_{0} A}{d}=\frac{(9)\left(8.85 \times 10^{-12}\right)(0.02)}{\left(8.85 \times 10^{-4}\right)} \\ & C_{B}=1.8 \times 10^{-9} \mathrm{~F} \end{aligned} $$
These two capacitors are in parallel. Therefore, net capacitance of the system is
$$ \begin{aligned} & C=C_{A}^{\prime}+C_{B}=(0.4+1.8) \times 10^{-9} \mathrm{~F} \\ & C=2.2 \times 10^{-9} \mathrm{~F} \end{aligned} $$
Charge stored in the system is $q=q_{A}=2.2 \times 10^{-7} \mathrm{C}$
Therefore, energy stored, $U=\frac{1}{2} \frac{q^{2}}{C}$
$$ U=\frac{1}{2} \frac{\left(2.2 \times 10^{-7}\right)^{2}}{\left(2.2 \times 10^{-9}\right)} \quad \text { or } \quad U=1.1 \times 10^{-5} \mathrm{~J} $$






