Electrostatics 5 Question 49
51. Two parallel plate capacitors $A$ and $B$ have the same separation $d=8.85 \times 10^{-4} m$ between the plates. The plate areas of $A$ and $B$ are $0.04 m^{2}$ and $0.02 m^{2}$ respectively. A slab of dielectric constant (relative permittivity) $K=9$ has dimensions such that it can exactly fill the space between the plates of capacitor $B$.
(1993, 7M)
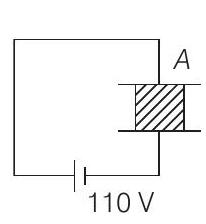
(i)
(ii)
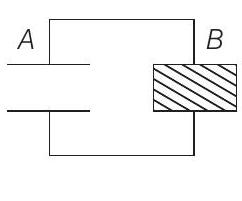
(iii) (a) The dielectric slab is placed inside $A$ as shown in figure (i) $A$ is then charged to a potential difference of $110 V$. Calculate the capacitance of $A$ and the energy stored in it.
(b) The battery is disconnected and then the dielectric slab is removed from $A$. Find the work done by the external agency in removing the slab from $A$.
(c) The same dielectric slab is now placed inside $B$, filling it completely. The two capacitors $A$ and $B$ are then connected as shown in figure (iii). Calculate the energy stored in the system.
Show Answer
Solution:
- (a) Capacitor $A$ is a combination of two capacitors $C _K$ and $C _O$ in parallel. Hence,
$$ C _A=C _K+C _O=\frac{K \varepsilon _0 A}{d}+\frac{\varepsilon _0 A}{d}=(K+1) \frac{\varepsilon _0 A}{d} $$
Here, $A=0.02 m^{2}$. Substituting the values, we have
$$ \begin{aligned} & C _A=(9+1) \frac{8.85 \times 10^{-12}(0.02)}{\left(8.85 \times 10^{-4}\right)} \\ & C _A=2.0 \times 10^{-9} F \end{aligned} $$
Energy stored in capacitor $A$, when connected with a $110 V$ battery is
$$ \begin{aligned} & U _A=\frac{1}{2} C _A V^{2}=\frac{1}{2}\left(2 \times 10^{-9}\right)(110)^{2} \\ & U _A=1.21 \times 10^{-5} J \end{aligned} $$
(b) Charge stored in the capacitor
$$ q _A=C _A V=\left(2.0 \times 10^{-9}\right)(110) \Rightarrow q _A=2.2 \times 10^{-7} C $$
Now, this charge remains constant even after battery is disconnected. But when the slab is removed, capacitance of $A$ will get reduced. Let it be $C _A^{\prime}$
$$ \begin{aligned} C _A^{\prime}=\frac{\varepsilon _0(2 A)}{d} & =\frac{\left(8.85 \times 10^{-12}\right)(0.04)}{8.85 \times 10^{-4}} \\ C _A^{\prime} & =0.4 \times 10^{-9} F \end{aligned} $$
Energy stored in this case would be
$$ \begin{aligned} U _A^{\prime} & =\frac{1}{2} \frac{\left(q _A\right)^{2}}{C _A^{\prime}}=\frac{1}{2} \frac{\left(2.2 \times 10^{-7}\right)^{2}}{\left(0.4 \times 10^{-9}\right)} \\ U _A^{\prime} & =6.05 \times 10^{-5} J>U _A \end{aligned} $$
Therefore, work done to remove the slab would be
$$ \begin{array}{rlrl} & W=U _A^{\prime} \quad-U _A=(6.05-1.21) \times 10^{-5} J \\ \text { or } & W & =4.84 \times 10^{-5} J \end{array} $$
(c) Capacity of $B$ when filled with dielectric is
$$ \begin{aligned} & C _B=\frac{K \varepsilon _0 A}{d}=\frac{(9)\left(8.85 \times 10^{-12}\right)(0.02)}{\left(8.85 \times 10^{-4}\right)} \\ & C _B=1.8 \times 10^{-9} F \end{aligned} $$
These two capacitors are in parallel. Therefore, net capacitance of the system is
$$ \begin{aligned} & C=C _A^{\prime}+C _B=(0.4+1.8) \times 10^{-9} F \\ & C=2.2 \times 10^{-9} F \end{aligned} $$
Charge stored in the system is $q=q _A=2.2 \times 10^{-7} C$
Therefore, energy stored, $U=\frac{1}{2} \frac{q^{2}}{C}$
$$ U=\frac{1}{2} \frac{\left(2.2 \times 10^{-7}\right)^{2}}{\left(2.2 \times 10^{-9}\right)} \quad \text { or } \quad U=1.1 \times 10^{-5} J $$






