Electrostatics 5 Question 47
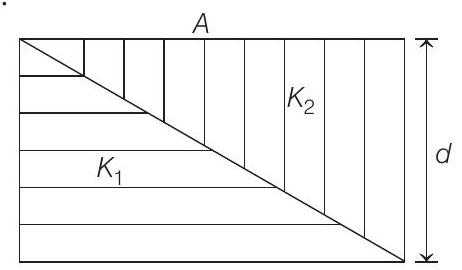
49. The capacitance of a parallel plate capacitor with plate area $A$ and separation $d$, is $C$. The space between the plates is filled with two wedges of dielectric constants $K_{1}$ and $K_{2}$ respectively (figure). Find the capacitance of the resulting capacitor.
Show Answer
Answer:
Correct Answer: 49. $C_R=\frac{C K_1 K_2}{K_2-K_1} \ln \frac{K_2}{K_1} \text { where, } C=\frac{\varepsilon_0 A}{d}$
Solution:
- Let length and breadth of the capacitor be $l$ and $b$ respectively and $d$ be the distance between the plates as shown in figure. Then, consider a strip at a distance $x$ of width $d x$.
Now, $Q R=x \tan \theta$
and $P Q=d-x \tan \theta$
where, $\tan \theta=d / l$
Capacitance of $P Q$
$$ \begin{gathered} C_{1}=\frac{K_{1} \varepsilon_{0}(b d x)}{d-x \tan \theta}=\frac{K_{1} \varepsilon_{0}(b d x)}{d-\frac{x d}{l}} \\ C_{1}=\frac{K_{1} \varepsilon_{0} b l d x}{d(l-x)}=\frac{K_{1} \varepsilon_{0} A(d x)}{d(l-x)} \end{gathered} $$
and $\quad C_{2}=$ capacitance of $Q R=\frac{K_{2} \varepsilon_{0} b(d x)}{x \tan \theta}$
$$ C_{2}=\frac{K_{2} \varepsilon_{0} A(d x)}{x d} \quad \tan \theta=\frac{d}{l} $$
Now, $C_{1}$ and $C_{2}$ are in series. Therefore, their resultant capacity $C_{0}$ will be given by
$$ \frac{1}{C_{0}}=\frac{1}{C_{1}}+\frac{1}{C_{2}} $$
Then, $\frac{1}{C_{0}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}=\frac{d(l-x)}{K_{1} \varepsilon_{0} A(d x)}+\frac{x \cdot d}{K_{2} \varepsilon_{0} A(d x)}$
$$ \begin{aligned} \frac{1}{C_ {0}} & =\frac{d}{\varepsilon_{0} A(d x)} \frac{l-x}{K_{1}}+\frac{x}{K_{2}} \\ & =\frac{d{K_{2}(l-x)+K_{1} x}}{\varepsilon_{0} A K_{1} K_{2}(d x)} \\ \therefore \quad C_{0} & =\frac{\varepsilon_{0} A K_{1} K_{2}}{d{K_{2}(l-x)+K_{1} x}} d x \\ C_{0} & =\frac{\varepsilon_{0} A K_{1} K_{2}}{d{K_{2} l+(K_{1}-K_{2}) x}} d x \end{aligned} $$
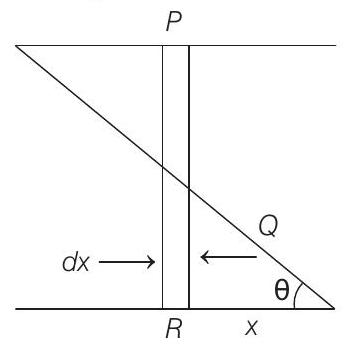
Now, the net capacitance of the given parallel plate capacitor is obtained by adding such infinitesimal capacitors placed parallel from $x=0$ to $x=l$
i.e. $\quad C_{R}=\int_{x=0}^{x=l} C_{0}=\int_{0}^{l} \frac{\varepsilon_{0} A K_{1} K_{2}}{d{K_{2} l+(K_{1}-K_{2}) x}} d x$
Finally we get $C_{R}=\frac{K_{1} K_{2} \varepsilon_{0} A}{(K_{2}-K_{1}) d} \ln \frac{K_{2}}{K_{1}}$
$$ =\frac{C K_{1} K_{2}}{K_{2}-K_{1}} \ln \frac{K_{2}}{K_{1}} \quad \text { where, } C=\frac{\varepsilon_{0} A}{d} $$
