Electrostatics 5 Question 47
49. The capacitance of a parallel plate capacitor with plate area $A$ and separation $d$, is $C$. The space between the plates is filled with two wedges of dielectric constants $K _1$ and $K _2$ respectively (figure). Find the capacitance of the resulting capacitor.
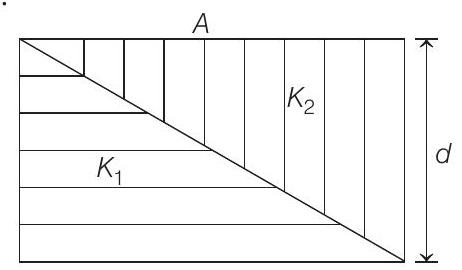
Show Answer
Solution:
- Let length and breadth of the capacitor be $l$ and $b$ respectively and $d$ be the distance between the plates as shown in figure. Then, consider a strip at a distance $x$ of width $d x$.
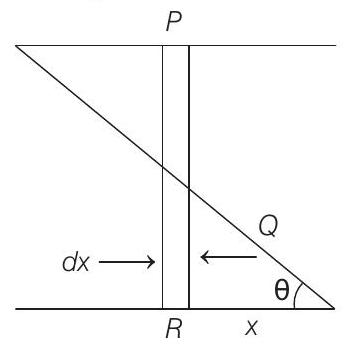
Now, $Q R=x \tan \theta$
and $P Q=d-x \tan \theta$
where, $\tan \theta=d / l$
Capacitance of $P Q$
$$ \begin{gathered} C _1=\frac{K _1 \varepsilon _0(b d x)}{d-x \tan \theta}=\frac{K _1 \varepsilon _0(b d x)}{d-\frac{x d}{l}} \\ C _1=\frac{K _1 \varepsilon _0 b l d x}{d(l-x)}=\frac{K _1 \varepsilon _0 A(d x)}{d(l-x)} \end{gathered} $$
and $\quad C _2=$ capacitance of $Q R=\frac{K _2 \varepsilon _0 b(d x)}{x \tan \theta}$
$$ C _2=\frac{K _2 \varepsilon _0 A(d x)}{x d} \quad \tan \theta=\frac{d}{l} $$
Now, $C _1$ and $C _2$ are in series. Therefore, their resultant capacity $C _0$ will be given by
$$ \frac{1}{C _0}=\frac{1}{C _1}+\frac{1}{C _2} $$
Then, $\frac{1}{C _0}=\frac{1}{C _1}+\frac{1}{C _2}=\frac{d(l-x)}{K _1 \varepsilon _0 A(d x)}+\frac{x \cdot d}{K _2 \varepsilon _0 A(d x)}$
$$ \begin{aligned} \frac{1}{C _0} & =\frac{d}{\varepsilon _0 A(d x)} \frac{l-x}{K _1}+\frac{x}{K _2} \\ & =\frac{d{K _2(l-x)+K _1 x }}{\varepsilon _0 A K _1 K _2(d x)} \\ \therefore \quad C _0 & =\frac{\varepsilon _0 A K _1 K _2}{d{K _2(l-x)+K _1 x }} d x \\ C _0 & =\frac{\varepsilon _0 A K _1 K _2}{d{K _2 l+\left(K _1-K _2\right) x }} d x \end{aligned} $$
Now, the net capacitance of the given parallel plate capacitor is obtained by adding such infinitesimal capacitors placed parallel from $x=0$ to $x=l$
i.e. $\quad C _R=\int _{x=0}^{x=l} C _0=\int _0^{l} \frac{\varepsilon _0 A K _1 K _2}{d{K _2 l+\left(K _1-K _2\right) x }} d x$
Finally we get $C _R=\frac{K _1 K _2 \varepsilon _0 A}{\left(K _2-K _1\right) d} \ln \frac{K _2}{K _1}$
$$ =\frac{C K _1 K _2}{K _2-K _1} \ln \frac{K _2}{K _1} \quad \text { where, } C=\frac{\varepsilon _0 A}{d} $$






