Electrostatics 5 Question 46
48. Two capacitors $A$ and $B$ with capacities $3 \mu \mathrm{F}$ and $2 \mu \mathrm{F}$ are charged to a potential difference of $100 \mathrm{~V}$ and $180 \mathrm{~V}$ respectively. The plates of the capacitors are connected as shown in the figure with one wire of each capacitor free. The upper plate of $A$ is positive and that of $B$ is negative. An uncharged $2 \mu \mathrm{F}$ capacitor $C$ with lead wires falls on the free ends to complete the circuit. Calculate
$(1997,5 M)$
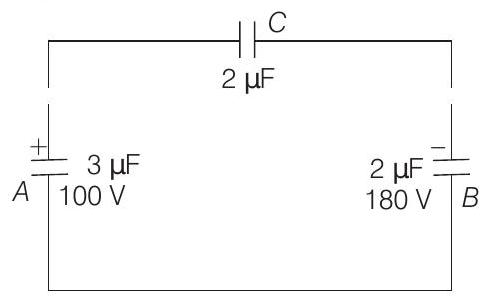
(a) the final charge on the three capacitors and
(b) the amount of electrostatic energy stored in the system before and after completion of the circuit.
Show Answer
Answer:
Correct Answer: 48. (a) $q_1=90 \mu \mathrm{C}, q_2=210 \mu \mathrm{C}, q_3=150 \mu \mathrm{C}$
(b) (i) $U_i=47.4 \mathrm{~mJ}$
(ii) $U_f=18 \mathrm{~mJ}$
Solution:
- (a) Charge on capacitor $A$, before joining with an uncharged capacitor
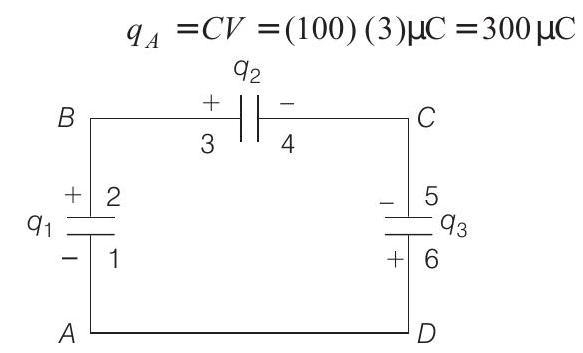
Similarly, charge on capacitor $B$
$$ q_{B}=(180)(2) \mu \mathrm{C}=360 \mu \mathrm{C} $$
Let $q_{1}, q_{2}$ and $q_{3}$ be the charges on the three capacitors after joining them as shown in figure.
$\left(q_{1}, q_{2}\right.$ and $q_{3}$ are in microcoulombs)
From conservation of charge
Net charge on plates 2 and 3 before joining $=$ net charge after joining
$$ \therefore \quad 300=q_{1}+q_{2} $$
Similarly, net charge on plates 4 and 5 before joining
$=$ net charge after joining $-360=-q_{2}-q_{3}$
or $\quad 360=q_{2}+q_{3}$
Applying Kirchhoff’s second law in closed loop $A B C D A$
$$ \begin{aligned} \frac{q_{1}}{3}-\frac{q_{2}}{2}+\frac{q_{3}}{2} & =0 \\ \text { or } \quad 2 q_{1}-3 q_{2}+3 q_{3} & =0 \end{aligned} $$
Solving Eqs. (i), (ii) and (iii), we get
$$ \begin{array}{ll} q_{1} & =90 \mu \mathrm{C}, q_{2}=210 \mu \mathrm{C} \\ \text { and } \quad q_{3} & =150 \mu \mathrm{C} \end{array} $$
(b) (i) Electrostatic energy stored before, completing the circuit
$$ \begin{gathered} U_{i}=\frac{1}{2}\left(3 \times 10^{-6}\right)(100)^{2}+\frac{1}{2}\left(2 \times 10^{-6}\right)(180)^{2} \\ \because U=\frac{1}{2} C V^{2} \\ =4.74 \times 10^{-2} \mathrm{~J} \text { or } U_{i}=47.4 \mathrm{~mJ} \end{gathered} $$
(ii) Electrostatic energy stored after, completing the circuit
$$ \begin{aligned} U_{f}= & \frac{1}{2} \frac{\left(90 \times 10^{-6}\right)^{2}}{\left(3 \times 10^{-6}\right)}+\frac{1}{2} \frac{\left(210 \times 10^{-6}\right)^{2}}{\left(2 \times 10^{-6}\right)} \\ & +\frac{1}{2} \frac{\left(150 \times 10^{-6}\right)^{2}}{\left(2 \times 10^{-6}\right)} \quad U=\frac{1}{2} \frac{q^{2}}{C} \\ & =1.8 \times 10^{-2} \mathrm{~J} \quad \text { or } \quad U_{f}=18 \mathrm{~mJ} \end{aligned} $$
