Electrostatics 5 Question 33
35. A parallel plate capacitor of capacitance
(a) zero
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 35. (b)
Solution:
- The diagramatic representation of given problem is shown in figure.
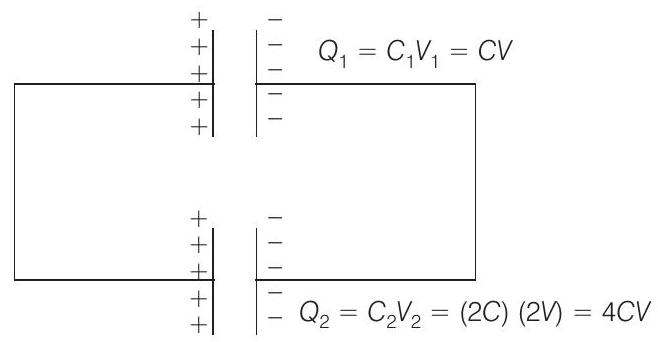
The net charge shared between the two capacitors is
The two capacitors will have the same potential, say
The net capacitance of the parallel combination of the two capacitors will be
The potential difference across the capacitors will be
The electrostatic energy of the capacitors will be






