Electrostatics 5 Question 20
22. In the given circuit, charge $Q_{2}$ on the $2 \mu \mathrm{F}$ capacitor changes as $C$ is varied from $1 \mu \mathrm{F}$ to $3 \mu \mathrm{F} . Q_{2}$ as a function of $C$ is given properly by (figures are drawn schematically and are not to scale)
(2015 Main)
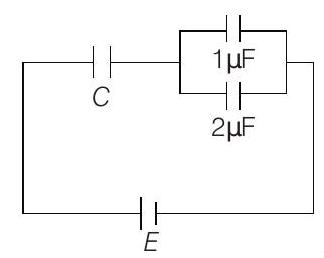
(a)
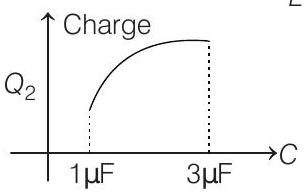
(b)
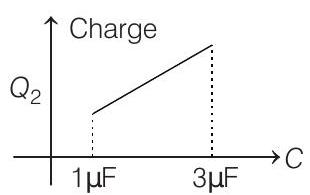
(c)
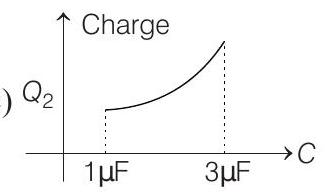
(d)
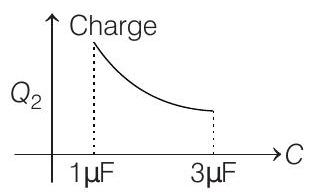
Show Answer
Answer:
Correct Answer: 22. (a)
Solution:
- Resultant of $1 \mu \mathrm{F}$ and $2 \mu \mathrm{F}$ is $3 \mu \mathrm{F}$. Now in series, potential difference distributes in inverse ratio of capacity.
$\therefore \quad \frac{V_{3 \mu \mathrm{F}}}{V_{c}}=\frac{c}{3} \quad$ or $\quad V_{3 \mu \mathrm{F}}=\frac{c}{c+3} E$
This is also the potential difference across $2 \mu \mathrm{F}$.
$ \begin{array}{ll} \therefore & Q_{2}=(2 \mu \mathrm{F})\left(V_{2 \mu \mathrm{F}}\right) \\ \text { or } & Q_{2}=\frac{2 c E}{c+3}=\frac{2}{1+\frac{3}{c}} E \end{array} $
From this expression of $Q_{2}$, we can see that $Q_{2}$ will increase with increase in the value of $c$ (but not linearly). Therefore, only options (a) and (b) may be correct.
Further, $\frac{d}{d c}\left(Q_{2}\right)=2 E \frac{(c+3)-c}{(c+3)^{2}}=\frac{6 E}{(c+3)^{2}}$
$=$ Slope of $Q_{2}$ verus $c$ graph
i.e. slope of $Q_{2}$ versus $c$ graph decreases with increase in the value of $c$. Hence, the correct graph is (a).
