Electrostatics 5 Question 12
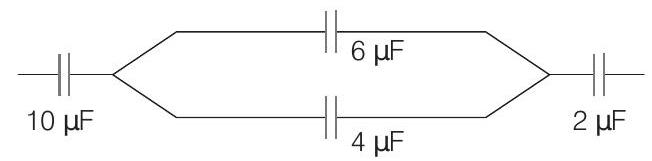
13. In the figure shown below, the charge on the left plate of the $10 \mu \mathrm{F}$ capacitor is $-30 \mu \mathrm{C}$. The charge on the right plate of the $6 \mu \mathrm{F}$ capacitor is
(Main 2019, 11 Jan I)
(a) $+12 \mu \mathrm{C}$
(b) $+18 \mu \mathrm{C}$
(c) $-12 \mu \mathrm{C}$
(d) $-18 \mu \mathrm{C}$
Show Answer
Answer:
Correct Answer: 13. (b)
Solution:
- Applying the concept of charge conservation on isolated plates of $10 \mu \mathrm{F}, 6 \mu \mathrm{F}$ and $4 \mu \mathrm{F}$. Since, $6 \mu \mathrm{F}$ and $4 \mu \mathrm{F}$ are in parallel, so total charge on this combination will be $30 \mu \mathrm{C}$.
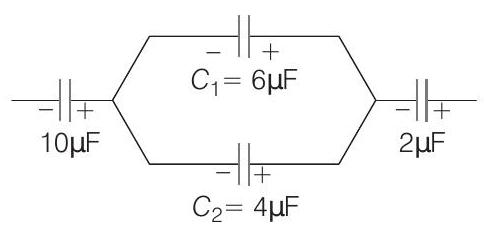
$\therefore$ Charge on $6 \mu \mathrm{F}$, capacitor
$ =\frac{C_{1}}{C_{1}+C_{2}} \quad q=\frac{6}{6+4} \times 30=18 \mu \mathrm{C} $
Since, the charge has been asked on the right plate of the capacitor. Thus, it would be $+18 \mu \mathrm{C}$.
Alternative method
Let charge on $6 \mu \mathrm{F}$ capacitor is $q \mu \mathrm{C}$.
Now, $V$ at $6 \mu \mathrm{F}=V$ at $4 \mu \mathrm{F}$
$ \begin{aligned} & \therefore \quad \frac{q}{6 \mu \mathrm{F}}=\frac{30-q}{4 \mu \mathrm{F}} \\ & (\because V=q / C) \\ & \Rightarrow \quad 4 q=-6 q+180 \\ & \Rightarrow \quad q=18 \mu \mathrm{C} \text {. } \end{aligned} $






