Electrostatics 5 Question 11
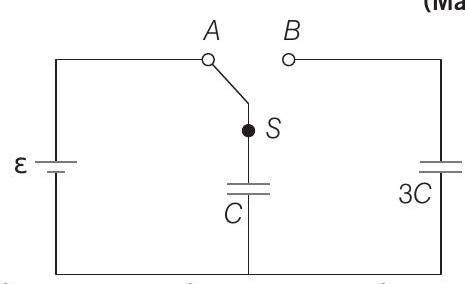
12. In the figure shown, after the switch ’ $S$ ’ is turned from position ’ $A$ ’ to position ’ $B$ ‘, the energy dissipated in the circuit in terms of capacitance ’ $C$ ’ and total charge ’ $Q$ ’ is
(a) $\frac{3}{4} \cdot \frac{Q^{2}}{C}$
(b) $\frac{5}{8} \cdot \frac{Q^{2}}{C}$
(c) $\frac{1}{8} \cdot \frac{Q^{2}}{C}$
(d) $\frac{3}{8} \cdot \frac{Q^{2}}{C}$
Show Answer
Answer:
Correct Answer: 12. (d)
Solution:
- In position ’ $A$ ’ of switch, we have a capacitor joined with battery.
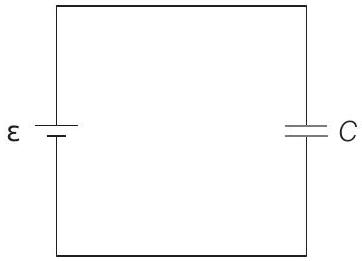
So, energy stored in position
$ U_{1}=\frac{1}{2} C \varepsilon^{2} $
When switch is turned to position $B$, we have a charged capacitor joined to an uncharged capacitor.
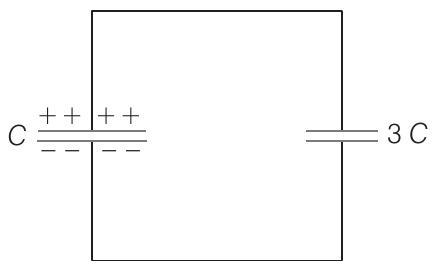
Common potential in steady state will be
$ V=\frac{\text { total charge }}{\text { total capacity }}=\frac{C \varepsilon}{4 C}=\frac{\varepsilon}{4} $
Now, energy stored will be
$ \begin{aligned} U_{2} & =\frac{1}{2}\left(C_{\mathrm{eq}}\right)\left(V_{\text {common }}\right)^{2} \\ & =\frac{1}{2} 4 C \times \frac{\varepsilon^{2}}{4}=\frac{1}{8} C \varepsilon^{2} \end{aligned} $
So, energy dissipated is
$ \begin{aligned} \Delta U & =U_{1}-U_{2}=\frac{1}{2} C \varepsilon^{2}-\frac{1}{8} C \varepsilon^{2} \\ & =\frac{3}{8} C \varepsilon^{2}=\frac{3}{8} C \frac{Q}{C}^{2}=\frac{3}{8} \cdot \frac{Q^{2}}{C} \end{aligned} $
