Electrostatics 5 Question 1
1. In the given circuit, the charge on $4 \mu \mathrm{F}$ capacitor will be
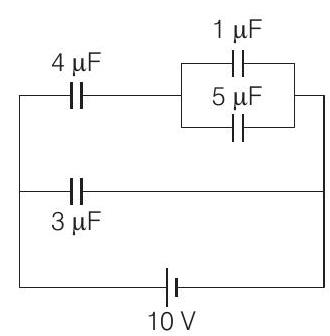
(Main 2019, 12 April II)
(a) $5.4 \mu \mathrm{C}$
(b) $9.6 \mu \mathrm{C}$
(c) $13.4 \mu \mathrm{C}$
(d) $24 \mu \mathrm{C}$
Show Answer
Answer:
Correct Answer: 1. (d)
Solution:
- Given circuit is
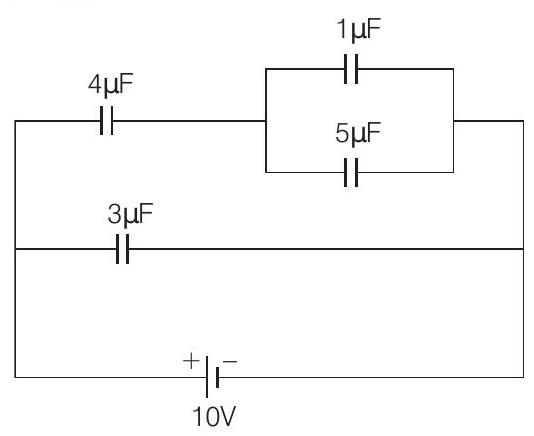
In parallel, $C_{\mathrm{eq}}=5+1=6 \mu \mathrm{F}$
and in series, $C_{\mathrm{eq}}^{\prime}=\frac{6 \times 4}{6+4}=2.4 \mu \mathrm{F}$
This is equivalent to
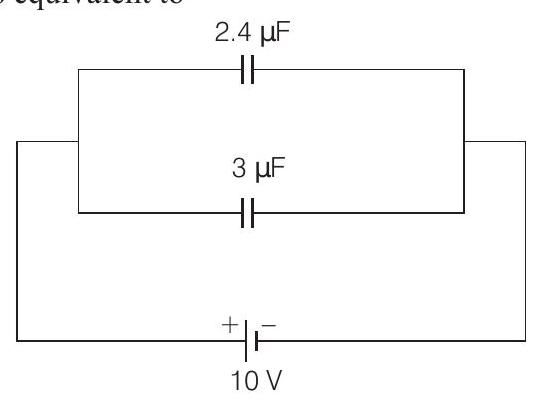
So, potential difference across upper branch $=10 \mathrm{~V}$ Using, $Q=C \times V$, charge delivered to upper branch is
$ \begin{aligned} Q & =C_{\mathrm{eq}}^{\prime} \cdot V=2.4 \mu \mathrm{F} \times 10 \mathrm{~V} \\ & =24 \mu \mathrm{C} \end{aligned} $
As we know, in series connection, same charge is shared by capacitors, so charge on $4 \mu \mathrm{F}$ capacitor and $6 \mu \mathrm{F}$ capacitor would be same,
i.e.,
$ Q_{4 \mu \mathrm{F}}^{\prime}=24 \mu \mathrm{C} $
Alternate Solution
The circuit obtained,
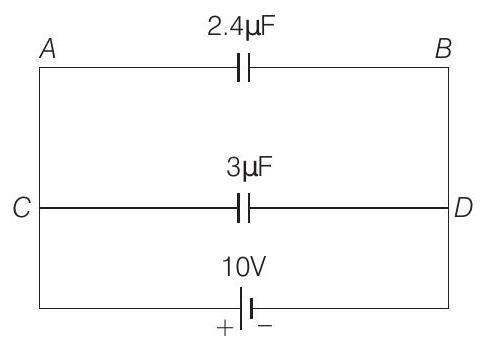
This can be further simplified as, $2.4 \mu \mathrm{F}$ and $3 \mu \mathrm{F}$ are in parallel.
So, net capacitance, $C_{\text {net }}=2.4+3=5.4 \mu \mathrm{F}$
Net charge flow through circuit,
$ Q=C_{\mathrm{net}} V=5.4 \times 10=54 \mu \mathrm{C} $
$\therefore$ This charge will be distributed in the ratio of capacitance in the two branches $A B$ and $C D$ as
$ \frac{Q_{1}}{Q_{2}}=\frac{2.4}{3}=\frac{4}{5} \Rightarrow 9 x=54 \mu \mathrm{C} \text { or } x=6 \mu \mathrm{C} $
$\therefore$ Charge on $4 \mu \mathrm{F}$ capacitor is $=4 \times 6 \mu \mathrm{C}=24 \mu \mathrm{C}$






