Electrostatics 5 Question 1
1. In the given circuit, the charge on $4 \mu F$ capacitor will be
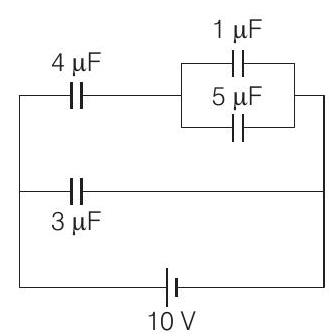
(Main 2019, 12 April II)
(a) $5.4 \mu C$
(b) $9.6 \mu C$
(c) $13.4 \mu C$
(d) $24 \mu C$
Show Answer
Answer:
Correct Answer: 1. (c)
Solution:
- Given circuit is
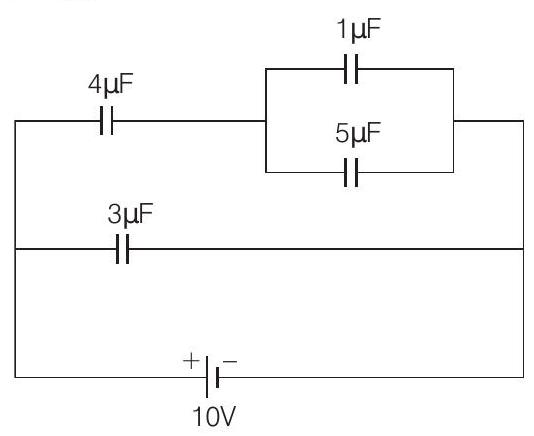
In parallel, $C _{eq}=5+1=6 \mu F$
and in series, $C _{eq}^{\prime}=\frac{6 \times 4}{6+4}=2.4 \mu F$
This is equivalent to
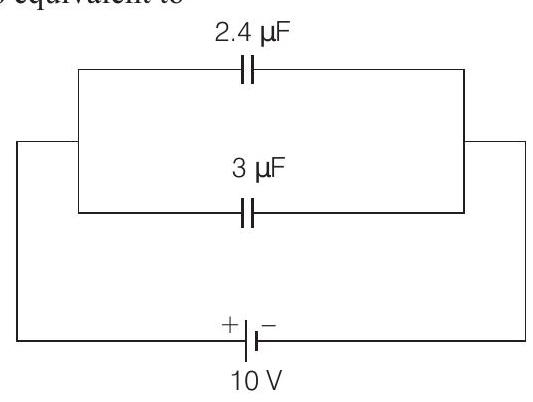
So, potential difference across upper branch $=10 V$ Using, $Q=C \times V$, charge delivered to upper branch is
$$ \begin{aligned} Q & =C _{eq}^{\prime} \cdot V=2.4 \mu F \times 10 V \\ & =24 \mu C \end{aligned} $$
As we know, in series connection, same charge is shared by capacitors, so charge on $4 \mu F$ capacitor and $6 \mu F$ capacitor would be same,
i.e.,
$$ Q _{4 \mu F}^{\prime}=24 \mu C $$
Alternate Solution
The circuit obtained,
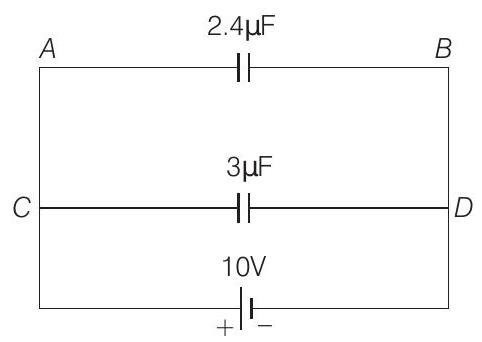
This can be further simplified as, $2.4 \mu F$ and $3 \mu F$ are in parallel.
So, net capacitance, $C _{\text {net }}=2.4+3=5.4 \mu F$
Net charge flow through circuit,
$$ Q=C _{net} V=5.4 \times 10=54 \mu C $$
$\therefore$ This charge will be distributed in the ratio of capacitance in the two branches $A B$ and $C D$ as
$$ \frac{Q _1}{Q _2}=\frac{2.4}{3}=\frac{4}{5} \Rightarrow 9 x=54 \mu C \text { or } x=6 \mu C $$
$\therefore$ Charge on $4 \mu F$ capacitor is $=4 \times 6 \mu C=24 \mu C$






