Electrostatics 4 Question 7
7. An electric dipole has a fixed dipole moment $\mathbf{P}$, which makes angle $\theta$ with respect to $\mathrm{X}$-axis. When subjected to an electric field $\mathbf{E} _ {1}=E \hat{\mathbf{i}}$, it experiences a torque $\mathbf{T} _ {1}=\pi \hat{\mathbf{k}}$. When subjected to another electric field $\mathbf{E} _ {2}=\sqrt{3} E _ {1} \hat{\mathbf{j}}$, it experiences a torque $\mathbf{T} _ {2}=-\mathbf{T} _ {1}$. The angle $\theta$ is
(2017 Main)
(a) $45^{\circ}$
(b) $60^{\circ}$
(c) $90^{\circ}$
(d) $30^{\circ}$
Show Answer
Answer:
Correct Answer: 7. (b)
Solution:
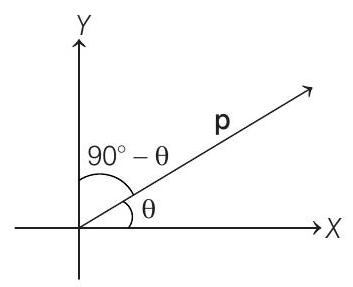
Torque applied on a dipole, $\tau=p E \sin \theta$
where, $\theta=$ angle between axis of dipole and electric field.
For electric field $E_{1}=E \hat{\mathbf{i}}$.
it means field is directed along positive $X$ direction, so angle between dipole and field will remain $\theta$, therefore torque in this direction
$ E_{1}=p E_{1} \sin \theta $
In electric field $E_{2}=\sqrt{3} E \hat{\mathrm{j}}$, it means field is directed along positive $Y$-axis, so angle between dipole and field will be $90-\theta$
Torque in this direction $T_{2}=p E \sin \left(90^{\circ}-\theta\right)$.
$ =p \sqrt{3} E_{1} \cos \theta $
According to question $\tau_{2}=-\tau_{1} \Rightarrow\left|\tau_{2}\right|=\left|\tau_{1}\right|$
$ \begin{aligned} & \therefore \quad p E_{1} \sin \theta=p \sqrt{3} E_{1} \cos \theta \\ & \tan \theta=\sqrt{3} \Rightarrow \tan \theta=\tan 60^{\circ} \\ & \therefore \quad \theta=60^{\circ} \end{aligned} $






