Electrostatics 4 Question 4
4. Charges $-q$ and $+q$ located at $A$ and $B$, respectively, constitute an electric dipole. Distance $A B=2 a, O$ is the mid point of the dipole and $O P$ is perpendicular to $A B$. A charge $Q$ is placed at $P$, where $O P=y$ and $y»2 a$. The charge $Q$ experiences an electrostatic force $F$.
(Main 2019, 10 Jan II)
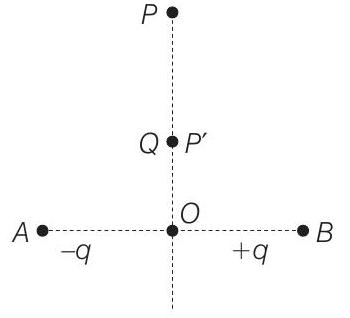
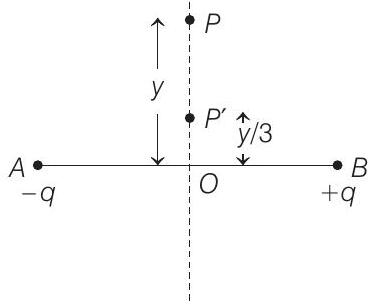
If $Q$ is now moved along the equatorial line to $P^{\prime}$ such that $O P^{\prime}=\Big(\frac{y}{3}\Big)$, the force on $Q$ will be close to $\Big(\frac{y}{3} \gg 2 a\Big)$
(a) $\frac{F}{3}$
(b) $3 F$
(c) $9 F$
(d) $27 F$
Show Answer
Answer:
Correct Answer: 4. (d)
Solution:
- Electric field on the equatorial line of a dipole at any point, which is at distance $r$ from the centre is given by
$ E=\frac{2 k P}{\left(r^{2}+a^{2}\right)^{3 / 2}} \cdots(i) $
where, $P$ is the dipole moment of the charges.
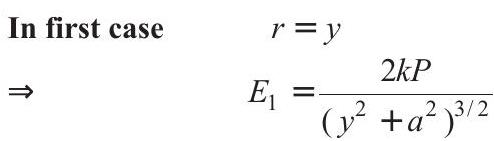
Here, $\quad y^{2}»a^{2}$
$\Rightarrow \quad y^{2}+a^{2} \approx y^{2}$
or
$ E_{1}=\frac{2 k P}{y^{3}} \cdots(ii) $
So, force on the charge in its position at $P$ will be
$ F=Q E_{1}=\frac{2 k P Q}{y^{3}} \cdots(iii) $
In second case $r=y / 3$
From Eq. (i), electric field at point $P^{\prime}$ will be
$ E_{2}=\frac{2 k P}{\frac{y}{3}^{2}+a^{2}} $
Again, $\frac{y}{3}»a \Rightarrow \frac{y}{3}^{2}+a^{2} \approx \frac{y}{3}^{2}$
$ \Rightarrow \quad E_{2}=\frac{2 k P}{(y / 3)^{3}} \Rightarrow E_{2}=27 \times \frac{2 k P}{y^{3}} $
Force on charge in this position,
$ F^{\prime}=Q E_{2}=27 \times \frac{2 k P Q}{y^{3}} \cdots(iv) $
From Eqs. (iii) and (iv), we get
$ F^{\prime}=27 F $






