Electrostatics 3 Question 2
2. A solid conducting sphere, having a charge $Q$, is surrounded by an uncharged conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be $V$. If the shell is now given a charge of $-4 Q$, the new potential difference between the same two surfaces is
(a) $-2 V$
(b) $2 \mathrm{~V}$
(c) $4 V$
(d) $V$
Show Answer
Answer:
Correct Answer: 2. (d)
Solution:
- Initially when uncharged shell encloses charge $Q$, charge distribution due to induction will be as shown,
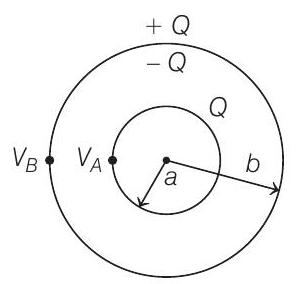
The potential on surface of inner shell is
$ V_{A}=\frac{k Q}{a}+\frac{k(-Q)}{b}+\frac{k Q}{b} $
where, $k$ =proportionality constant.
Potential on surface of outer shell is
$ V_{B}=\frac{k Q}{b}+\frac{k(-Q)}{b}+\frac{k Q}{b} $
Then, potential difference is
$ \Delta V_{A B}=V_{A}-V_{B}=k Q \frac{1}{a}-\frac{1}{b} $
Given,
$ \Delta V_{A B}=V $
So, $\quad k Q \frac{1}{a}-\frac{1}{b}=V$
Finally after giving charge $-4 Q$ to outer shell, potential difference will be
$ \begin{aligned} \Delta V_{A B}=V_{A}-V_{B} & =\frac{k Q}{a}+\frac{k(-4 Q)}{b}-\frac{k Q}{b}+\frac{k(-4 Q)}{b} \\ & =k Q \frac{1}{a}-\frac{1}{b}=V \quad \text { [from Eq. (iii)]} \end{aligned} $
Hence, we obtain that potential difference does not depend on the charge of outer sphere, hence potential difference remains same.






