Electrostatics 3 Question 2
2. A solid conducting sphere, having a charge $Q$, is surrounded by an uncharged conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be $V$. If the shell is now given a charge of $-4 Q$, the new potential difference between the same two surfaces is
(a) $-2 V$
(b) $2 V$
(c) $4 V$
(d) $V$
Show Answer
Answer:
Correct Answer: 2. (c)
Solution:
- Initially when uncharged shell encloses charge $Q$, charge distribution due to induction will be as shown,
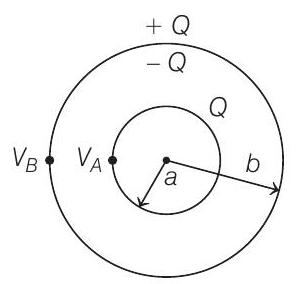
The potential on surface of inner shell is
$$ V _A=\frac{k Q}{a}+\frac{k(-Q)}{b}+\frac{k Q}{b} $$
where, $k$ =proportionality constant.
Potential on surface of outer shell is
$$ V _B=\frac{k Q}{b}+\frac{k(-Q)}{b}+\frac{k Q}{b} $$
Then, potential difference is
$$ \Delta V _{A B}=V _A-V _B=k Q \frac{1}{a}-\frac{1}{b} $$
Given,
$$ \Delta V _{A B}=V $$
So, $\quad k Q \frac{1}{a}-\frac{1}{b}=V$
Finally after giving charge $-4 Q$ to outer shell, potential difference will be
$$ \begin{aligned} \Delta V _{A B}=V _A-V _B & =\frac{k Q}{a}+\frac{k(-4 Q)}{b}-\frac{k Q}{b}+\frac{k(-4 Q)}{b} \\ & =k Q \frac{1}{a}-\frac{1}{b}=V \quad \text { [from Eq. } \end{aligned} $$
Hence, we obtain that potential difference does not depend on the charge of outer sphere, hence potential difference remains same.
